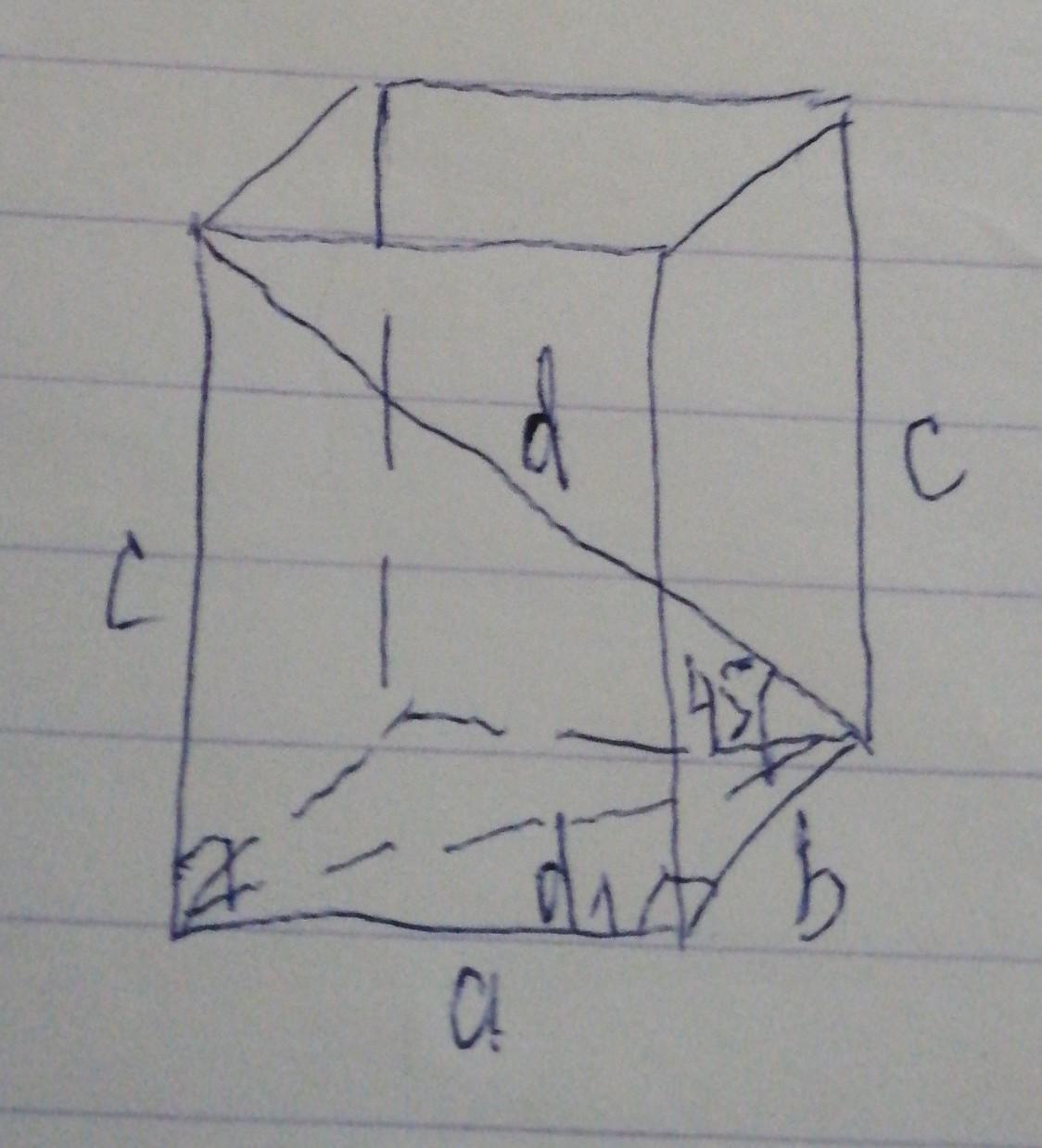
В прямоугольном параллелепипеде одна из сторон основания равна 3 см. Диагональ параллелепипеда равна 5 см и образует с плоскостью основания угол 450. Найдите объем параллелепипеда.
Ответы
Відповідь: V пар = 15√7/4 см³ .
Пояснення:
V пар = a b c .
ABCDA₁B₁C₁D₁ - прямок. пар - пед ; АВ = 3 см ; B₁D = 5 см ;
∠BDB₁ = 45° . У прямок. ΔBDB₁ ВD = BB₁ , тому 2ВB₁² = B₁D² ; ---->
ВB₁² = 1/2 *B₁D² =25/2 ; ВD = BB₁ = 5/√2 см .
У прямок. ΔАBD AD = √( BD² - AB² ) = √( ( 5/√2 )² - 3² ) = √14/2 ( см ) .
V пар = √14/2 * 3 * 5/√2 = 15√7/4 ( см³ ) ; V пар = 15√7/4 см³ .
Объяснение:
V=a×b×c
а=3 см - Сторона основания
b - Cторона основания
с - Высота
d=5 см - диагональ параллеллепипеда
Альфа=45 градусов - угол между диагонлью
и плоскостью основания.
Решение :
V=a×b×c
d1 - диагональ основания
d1=c, т. к тр-к равнобедренный (<=45 градусов), прямоугольный :
По теореме Пифагора :
d²=d1²+c²=d1²+d1²=2d1²
5²=2d1²
d1²=25/2
d1=корень (25/2) =(5×корень2)/2 см
По теореме Пифагора :
b=корень (d1²-a²) =
=корень((5×корень2)/2)²-3²)=
=корень (25/2-9)=корень(7/2)=
=(корень7×корень2) /2=(корень 14)/2 см
V=3×(корень14)/2 ×(5×корень2)/2=
=(15×(корень28)) /4=(15×2×корень7) /4=
=(15×корень7)/2 см³
Ответ : (15×корень7) /2 см³