Предмет: Алгебра,
автор: Mozaika22818
Помогите решить задания, либо только 5 задания хотя бы, буду очень благодарен
Приложения:
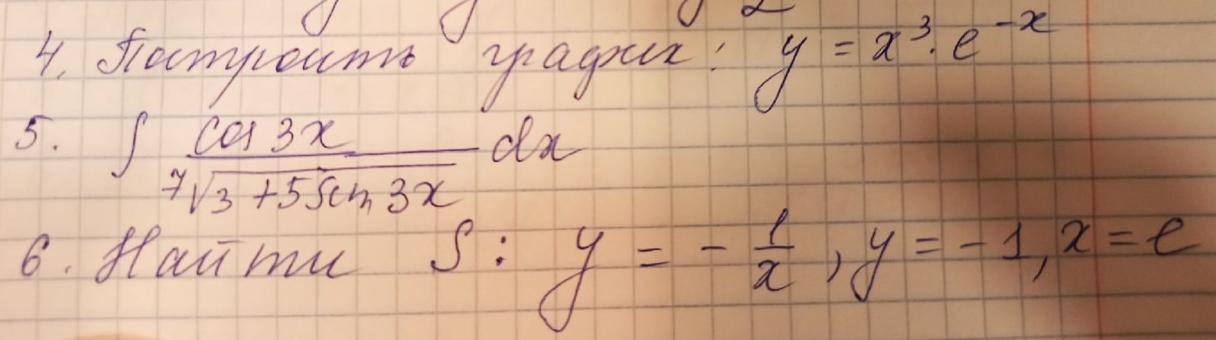
Ответы
Автор ответа:
1
Объяснение:
5.
6.
Ответ: S≈0,7183 кв.ед.
Приложения:
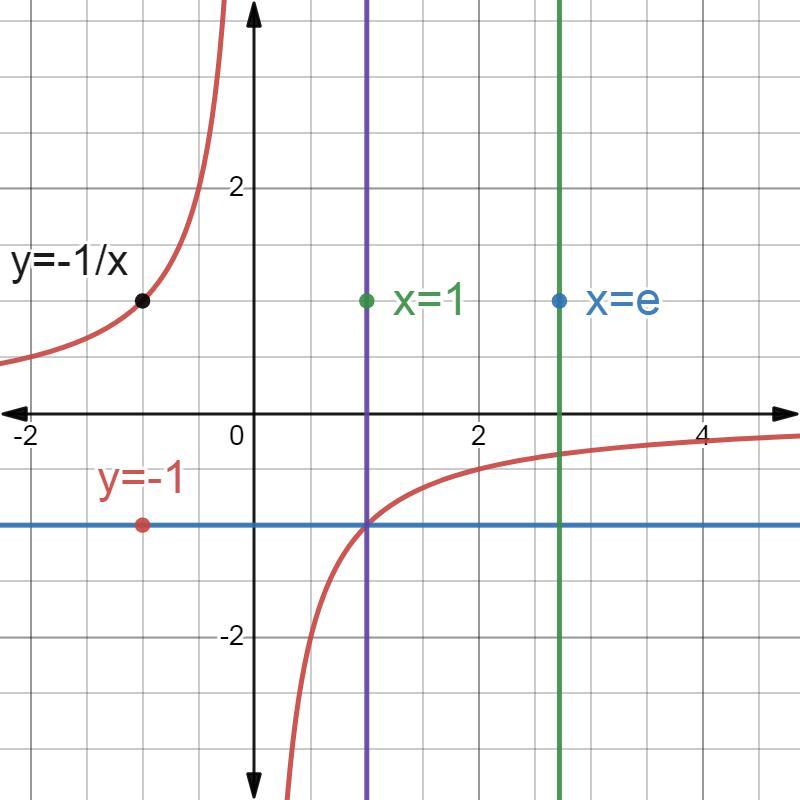
Похожие вопросы
Предмет: Окружающий мир,
автор: 2017zaichik
Предмет: Русский язык,
автор: nastyona2005
Предмет: Английский язык,
автор: Аноним
Предмет: Беларуская мова,
автор: mashaselvich91
Предмет: Английский язык,
автор: matvey6197