Помогите срочно! Даю 30 баллов, желательно с решением через дискриминант
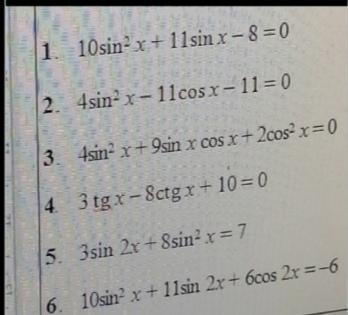
Ответы
Ответ:
1)
10sin²(x)+11sin(x)-8=0
sin(x)=t, |t|≤1
10t²+11t-8=0
D=121+320=441=21²
t1=(-11+21)/20=1/2
t2=-(11-21)/20=-1.6∉|t|≤1
sin(x)=1/2
x=(-1)^n *arcsin(1/2)+πn,n∈Z
x=(-1)^n *π/6 +πn, n∈Z
2)
4sin²(x)-11cos(x)-11=0
4(1-cos²(x))-11cos(x)-11=0
4-4cos²(x)-11cos(x)-11=0
4cos²(x)+11cos(x)+7=0
cosx=t, |t|≤1
4t²+11t+7=0
D=121-112=9=3²
t1=(-11+3)/8=-1
t2=(-11-3)/8=-7/4∉|t|≤1
cos(x)=-1
x=π+2πn,n∈Z
3)
4sin²(x)+9sin(x)cos(x)+2cos²(x)=0 |:(cos²(x)≠0)
4tg²(x)+9tg(x)+2=0
tg(x)=t
4t²+9t+2=0
D=81-32=49=7²
t1=(-9+7)/8=-1/4
t2=(-9-7)/8=-2
tg(x)=-1/4
x=arctg(-1/4)+πn,n∈Z
x=-arctg1/4+πn,n∈Z
tg(x)=-2
x=arctg(-2)+πm,m∈Z
x=-arctg2+πm,m∈Z
4)
3tg(x)-8ctg(x)+10=0
3tg(x)-8(1/tg(x))+10=0 |*tg(x)≠0
3tg²(x)+10tg(x)-8=0
tg(x)=t
3t²+10t-8=0
D=100+96=196=14²
t1=(-10+14)/6=2/3
t2=(-10-14)/6=-4
tg(x)=2/3
x=arctg(2/3)+πn,n∈Z
tg(x)=-4
x=arctg(-4)+πm,m∈Z
x=-arctg4+πm,m∈Z
5)
3sin(2x)+8sin²(x)-7*1=0
6sin(x)cos(x)+8sin²(x)-7(cos²(x)+sin²(x))=0 |:cos²x≠0
6tg(x)+8tg²(x)-7-7tg²(x)=0
tg²(x)+6tg(x)-7=0
tg(x)=t
t²+6t-7=0
D=36+28=64=8²
t1=(-6+8)/2=1
t2=(-6-8)/2=-7
tg(x)=1
x=arctg(1)+πn,n∈Z
x=π/4 +πn,n∈Z
tg(x)=-7
x=arctg(-7)+πm,m∈Z
x=-arctg7+πm,m∈Z