Предмет: Математика,
автор: seryjgray
Прошу помощи. Теория вероятностей и математическая статистика
1) сократите дробь
2) решите уравнения
желательно с объяснением действий пж
Приложения:
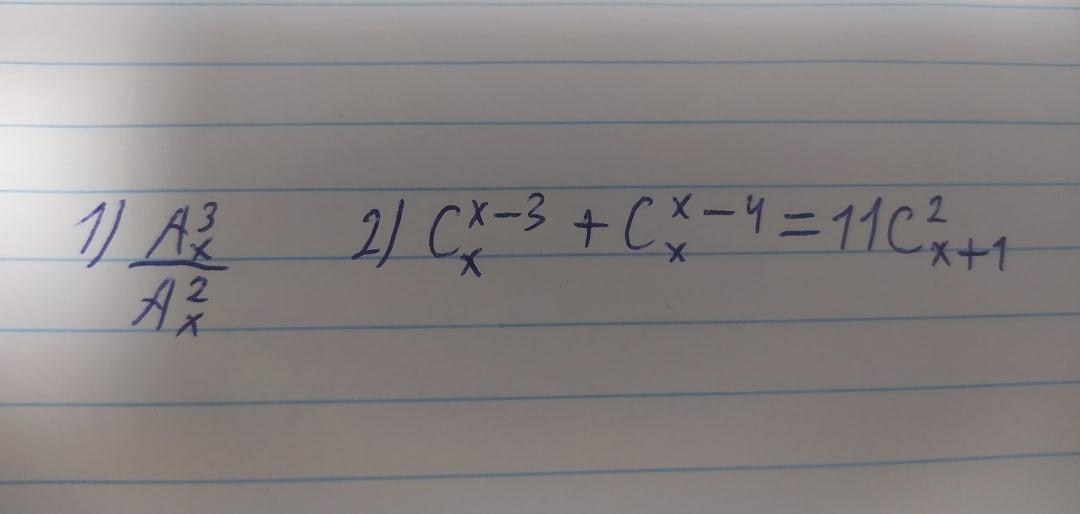
Ответы
Автор ответа:
2
Ответ:
1)
2)
Биноминальный коэффициент должен больше нуля или равно нулю, поэтому x≠-10.
Следовательно, ответ: x=13
Похожие вопросы
Предмет: Русский язык,
автор: irinkasarov
Предмет: Английский язык,
автор: анняэлпкмо
Предмет: Русский язык,
автор: sandreyanova20
Предмет: Математика,
автор: sizovkirill07