9. Углы треугольника относятся как 1:2:3, а сумма длин большей и меньшей сторон и равна 18 см. Найдите длину большей стороны (в см). 9. Углы треугольника относятся как 1 : 2 : 3 , а сумма длин большей и меньшей сторон и равна 18 см . Найдите длину большей стороны ( в см ) .
Ответы
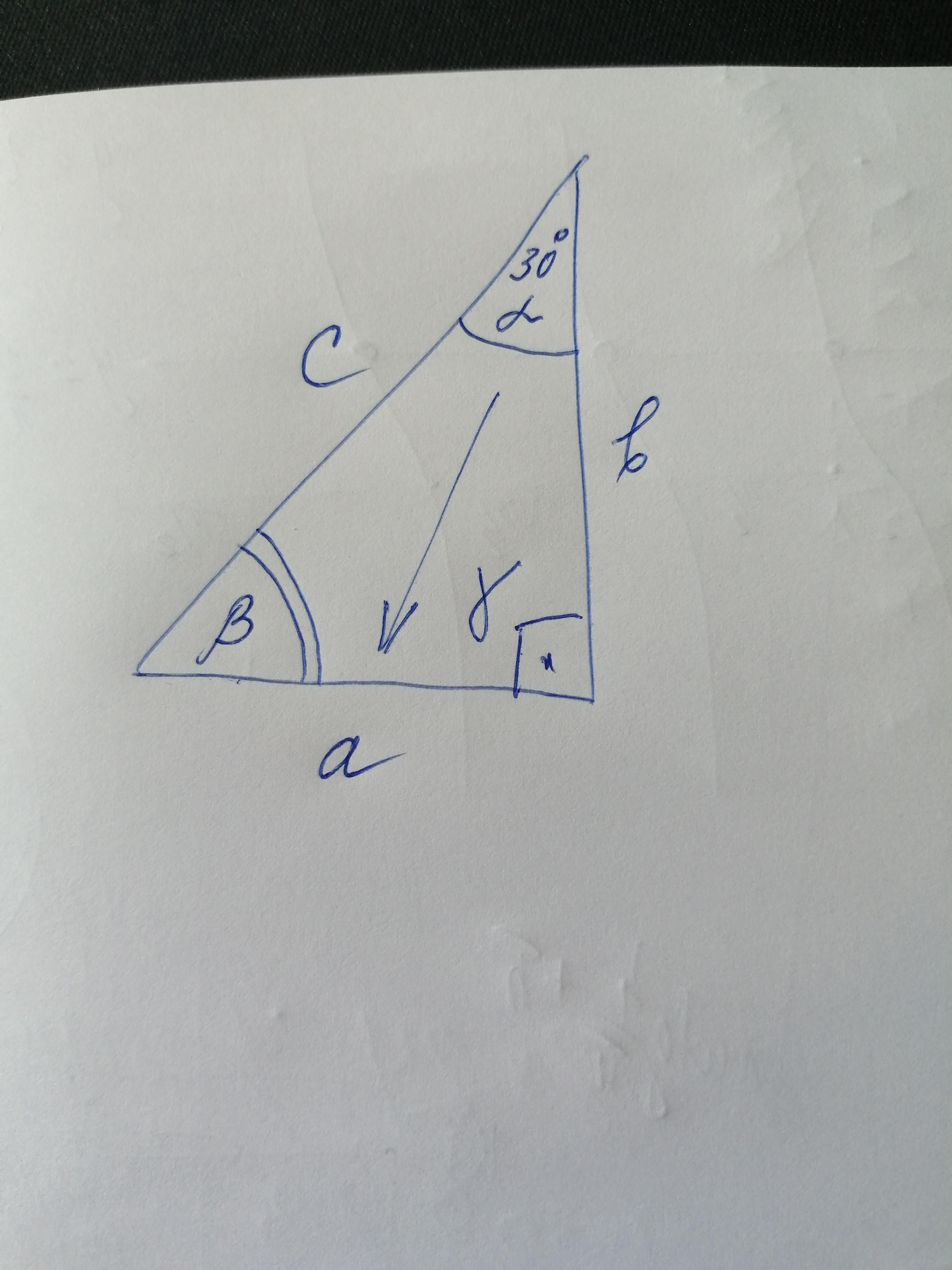
Решение смотри на фото

Решение:
Обозначим углы треугольника буквами α, β, γ. Тогда, по условию задачи, α:β:γ=1:2:3, значит, α=x°, β=2x°, γ=3x°.
По теореме о сумме углов треугольника, сумма углов треугольника равна 180°, поэтому, α+β+γ=180°
x+2x+3x=180°
6x=180°
x=180°:6
x=30° - мЕньший угол треугольника
γ=3*30°=90° - бОльший угол треугольника
В треугольнике против мЕньшего угла лежит мЕньшая сторона (обозначим её буквой "а") , а против бОльшего угла лежит бОльшая сторона (обозначим её буквой "с").
Данный треугольник является прямоугольным (т.к. у него один из углов равен 90°) с острым углом 30° Известно, что катет, лежащий против угла 30° равен половине гипотенузы. Получаем, что с = 2а.
По условию, а+с=18 см
a+2a=18
3a=18
a=18:3
a=6 см - мЕньшая сторона треугольника
с = 2а = 2*6 = 12 (см) - бОльшая сторна треугольника
Ответ: 12 см