Предмет: Геометрия,
автор: Anastosik
!!Терміново, допоможіть, будь ласка, обов'язково з розв'язком!!
Приложения:

Ответы
Автор ответа:
0
Ответ:
Sбок. = 16√389 см²
Объяснение:
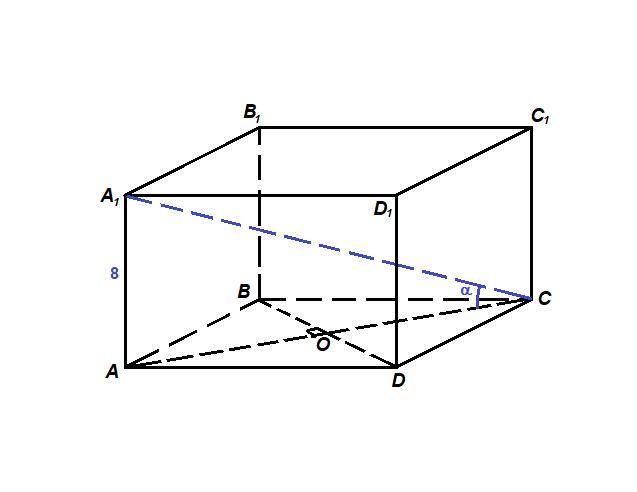
Дана прямая четырехугольная призма, ABCD - ромб.
АС = 17 см
BD = 10 см
АА₁ = 8 см
- Диагонали ромба взаимно перпендикулярны и делятся точкой пересечения пополам.
АО = 0,5 АС = 0,5 · 17 = 8,5 см
ВО = 0,5 BD = 0,5 · 10 = 5 см
ΔАОВ: ∠АОВ = 90°, по теореме Пифагора:
см
- Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.
см²
А₁С - большая диагональ призмы, АС - ее проекция на площадь основания.
∠А₁СА = α - искомый.
ΔА₁СА: ∠А₁АС = 90°,
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Ленккa
Предмет: Русский язык,
автор: ботерфляй
Предмет: Русский язык,
автор: Faisdesseriesdemots
Предмет: Русский язык,
автор: 666666782
Предмет: Химия,
автор: Phyodo