Задание приложено...
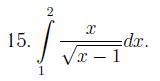
Ответы
Ответ:
Пошаговое объяснение:
По определению, записываем несобственный интеграл через односторонний предел и определенный интеграл —
Вычисляем определенный интеграл —
- Чтобы вычислить определенный интеграл, вначале нужно найти неопределенный —
- Преобразовываем интеграл, используя подстановку t = x - 1 —
- Используя
, преобразовываем выражение —
- Разделим дробь на 2 дроби —
- Упрощаем выражение —
- Используя свойство интегралов ∫ f (x) ± g (x) dx = ∫ f (x) dx ± ∫ g (x) dx —
- Используя
находим интеграл —
- Используя
находим интеграл —
- Производим обратную замену t = x - 1 —
- Вычисляем выражение —
- Упрощаем выражение —
- Подставляем значение интеграла обратно —
Вычисляем предел —
- а - 1 положителен, так как он стремится к 0 справа, следовательно |a - 1| = a - 1 —
- Вычисляем предел —
Упрощаем выражение —
- Сумма двух противоположных чисел равна 0 —
- Любое выражение, умноженное на 0, равно 0; также любой корень из 0 равен 0 —
- Удаление 0 не изменяет значение, убираем его из выражения; также любое выражение, умноженное на 0, равно 0 —
- Удаление 0 не изменяет значение, убираем его из выражения —
- Переводим в смешанное число —
Ответ:
Примечание:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
- несобственный интеграл 2 рода
Так как не определена в точке
.
Если существует конечный предел у несобственного интеграла, то данный интеграл является сходящимся.
Рассмотрим неопределенный интеграл .
----------------------------------------------------------------------------------------------------------
Замена:
----------------------------------------------------------------------------------------------------------
Для вычисления несобственного 2 рода воспользуемся двойной несобственной подстановкой при необходимости:
.