Предмет: Математика,
автор: Reideen
Задание приложено...
Приложения:
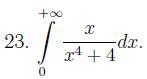
Ответы
Автор ответа:
1
Ответ:
111111111111111111111111111
Приложения:

Автор ответа:
0
Ответ:
Примечание:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
- несобственный интеграл 1 рода
Если существует предел существует конечный предел у несобственного интеграла, то данный интеграл является сходящимся.
Рассмотрим неопределенный интеграл .
-------------------------------------------------------------------------------------------------------
Замена:
--------------------------------------------------------------------------------------------------------
Для вычисления несобственного 1 рода воспользуемся двойной несобственной подстановкой:
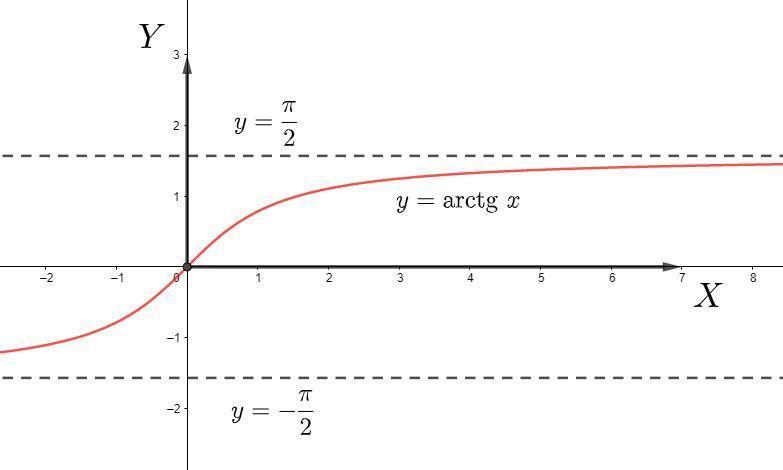
Так как асимптота графика при
это
, то
.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: princess119991
Предмет: Русский язык,
автор: 999121
Предмет: Русский язык,
автор: Savostyanova3
Предмет: Литература,
автор: sidorenkoilona2
Предмет: История,
автор: tdragan86