Предмет: Математика,
автор: vanymene228007
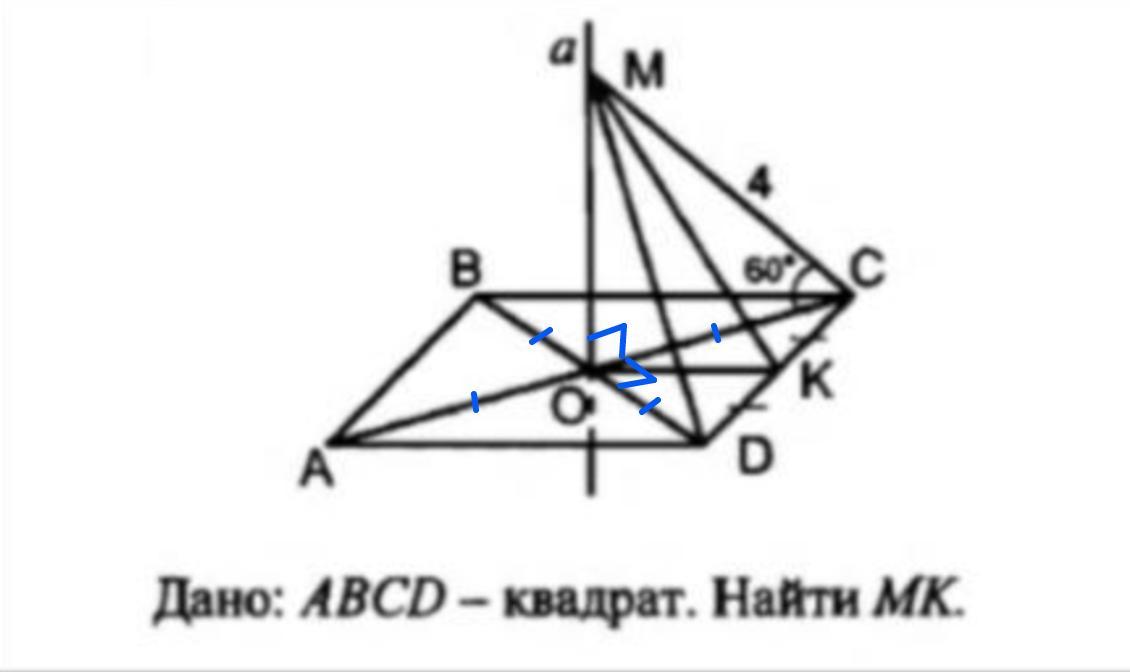
ПОМОГИТЕ ПОЖАЛУЙСТА.Точка М не лежить в площині (АВС). АBCD - квадрат. Знайти МК
Приложения:

Ответы
Автор ответа:
5
Ответ:
Отрезок МК равен √14 ед.
Пошаговое объяснение:
Точка М не лежит в плоскости (АВС). АBCD - квадрат. Найти МК.
Дано: АBCD - квадрат.
М ∉ АВС;
∠МСО = 60°; МС = 4.
DK = KC
Найти: МК.
Решение:
1. Рассмотрим ΔОМС - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ОМС = 90° - 60° = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
ОС = МС : 2 = 2
2. Рассмотрим ABCD - квадрат.
- Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам.
⇒ ОС = OD = 2
3. Рассмотрим Δ ОСD - прямоугольный, равнобедренный.
По теореме Пифагора найдем DC:
DC² = OC² + OD² = 4 + 4 = 8
DC = 2√2
DK = KC (условие) ⇒ DK = KC = √2
⇒ OK - медиана.
- В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.
⇒ ОК ⊥ DK.
4. Рассмотрим ΔКМС.
- Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
ОК ⊥ DK ⇒ МК ⊥ DC.
⇒ ΔКМС - прямоугольный.
По теореме Пифагора найдем МК:
МК² = МС² - КС² = 16 - 2 = 14
МК = √14
Отрезок МК равен √14 ед.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: cucia
Предмет: Русский язык,
автор: Лаsтик
Предмет: Русский язык,
автор: musha29
Предмет: Алгебра,
автор: natasha0987
Предмет: Биология,
автор: stdnkp