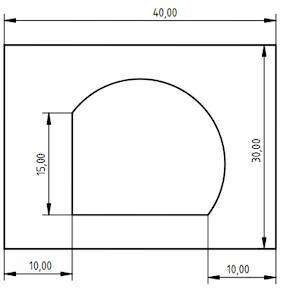
Вычислите периметр внутренней вырезанной фигуры, если известно, что дуга - это полуокружность.
Ответы
Ответ:
Площадь фигуры = 804,6875 ед².
Объяснение:
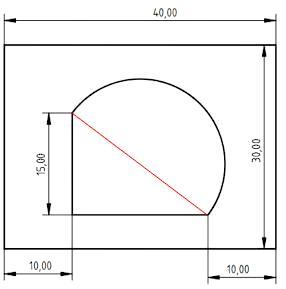
Проведём дополнительную (красную) линию.
Имеет 3 фигуры:
1. Прямоугольник площадью S =40×30 = 1200 ед².
2. Прямоугольный треугольник со сторонами a = 15 ед., b = 40-(10+10) = 20 ед.
Площадь прямоугольного треугольника S = 1/2 * a * b = 1/2 * 15 * 20 = 150 ед².
По теореме Пифагора:
Гипотенуза² (красная линия) = a² + b²
Гипотенуза² = 15² + 20²
Гипотенуза = √(225 + 400)
Гипотенуза = √625
Гипотенуза = 25 ед.
3. Полукруг с диаметром D = Гипотенузе = 25 ед.
⇒ Радиус R = D/2 = 25÷2 = 12,5 ед.
Площадь целого круга: S = πR² = 3,14 × 12,5² = 3,14 × 156,25 = 490,625 ед²
Площадь нашего полукруга S = S(круга) ÷ 2 = 490,625 ÷ 2 = 245,3125 ед².
Площадь нашей фигуры S = S(прямоугольника) - [S(треугольника) + S(полукруга)] = 1200 - [150 + 245,3125] = 1200 - 395,3125 = 804,6875 ед².
Длина окружности: L = 2πR = πD = 3,14 × 25 = 78,5 ед.
Длина полуокружности L = L(окружности) ÷ 2 = 78,5 ÷ 2 = 39,25 ед.
Периметр внутренней вырезанной фигуры:
P = a + b + L(полуокружности) = 15 + 20 + 39,25 = 74,25 ед.
Периметр внутренней вырезанной фигуры = 74,25 ед.
Объяснение:
Проведём дополнительную (красную) линию.
Имеет 2 фигуры:
1. Прямоугольный треугольник со сторонами a = 15 ед., b = 40-(10+10) = 20 ед.
По теореме Пифагора:
Гипотенуза² (красная линия) = a² + b²
Гипотенуза² = 15² + 20²
Гипотенуза = √(225 + 400)
Гипотенуза = √625
Гипотенуза = 25 ед.