Предмет: Математика,
автор: solka0000
розв'язати диференційне рівняння в повних диференціалах
рівняння на прикріпленому фото
Приложения:
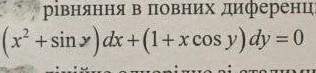
Ответы
Автор ответа:
1
Ответ:
Проверим, является ли заданное дифф.уравнение, уравнением в полных дифференциалах .
Получили, что . Поэтому заданное д.у. является д.у. в полных дифференциалах. И можно записать
.
Теперь найдём
Подставим найденное значение в выражение для
:
Ответ: общий интеграл .
Похожие вопросы
Предмет: Русский язык,
автор: Илья3в
Предмет: Русский язык,
автор: Сергейчук1
Предмет: Русский язык,
автор: NatashaPermen05
Предмет: Русский язык,
автор: awakes
Предмет: Английский язык,
автор: krytou742