Question

AB отрезок - это диаметр окружности с центром. На каждом радиусе OM окружности есть отрезок из Օ точки, длина которого равна расстоянию между точкой M и AB. Найдите множество ребер построенных сечений

Answer 1

Ответ:

Пусть радиус окружности будет R

значит АВ = 2R

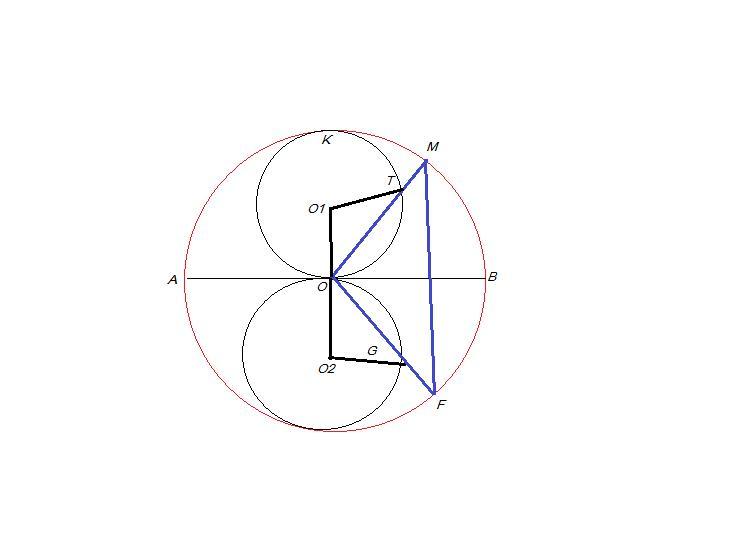
точка F — пропорциональная точке M  (AB)

По данным MH = OT, HF = OG

пусть  ∠MOH = $\alpha$

из  прям. треугольника MOH

МH= OM· sin∠MOH

значит MH = R·sin$\alpha$

поскольку MH=OT ⇔ OT=R·sin$\alpha$

замечаем что ОТ с центром О1 и с радиусом  $\frac{R}{2}$ --- дуга

По рисунку видно что ∠ТОО1 = 90°- ∠МOH = 90°- $\alpha$

треугольник ТОО1 равнобедренный ⇔ ОО1 = О1Т = $\frac{R}{2}$

∠TOO1 = ∠OTO1 = 90° - $\alpha$

так как сумма внутренних углов всех треугольников равна 180°

⇔

из треугольника TOO1

∠TOO1 - ∠OTO1 - ∠OO1T = 180°

⇒

∠OO1T = 180° - (∠TOO1 + ∠OTO1) = 180° - 90 - $\alpha$ + 90° - $\alpha$ = 2$\alpha$

В треугольнике ТОО1 по теорему косинусов  

$OT =\sqrt{OO1^{2}+O1T^{2}-2OO1 x O1T x cosOO1T }$

$OT =\sqrt{\frac{R^{2} }{4} +\frac{R^{2} }{4} - 2 x \frac{R^{2} }{4} x cos2\alpha } = R x \sqrt{\frac{1-cos2\alpha }{2} } = R x sin\alpha$

так как ОТ с радиусом $\frac{R}{2}$ - дуга (с центром О1)

⇔

ОG с радиусом $\frac{R}{2}$ - (дуга  с центром О2)

получается  что вершины отрезка OG принадлежат окружности  с центром О2 и с радиусом $\frac{R}{2}$