Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, люди добрые и не очень, с алгеброй
Приложения:
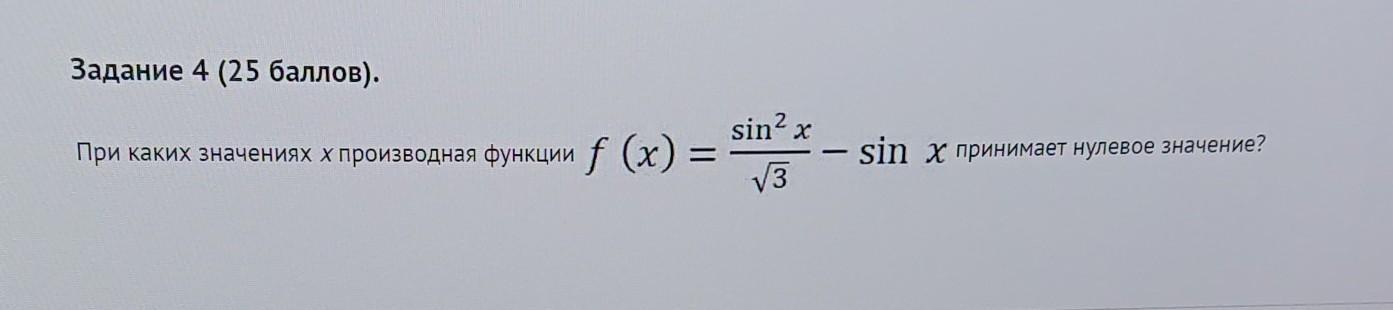
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Для начала найдем производную.
Теперь решим уравнение
#SPJ1
Автор ответа:
0
Відповідь:
Пояснення:
Похожие вопросы
Предмет: Українська література,
автор: Аноним
Предмет: Українська мова,
автор: kravchukalla
Предмет: Қазақ тiлi,
автор: АнГеЛоК31а
Предмет: Литература,
автор: Аноним
Предмет: История,
автор: facebookwrm1