решите, пожалуйста ,срочно
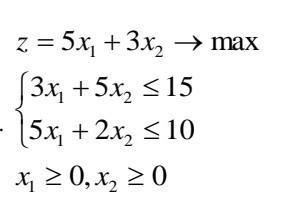
Ответы
Ответ:
максимальное значение целевой функции ≈ 12,3684
Пошаговое объяснение:
Это задача линейного программирования, которую мы буем решать графическим методом.
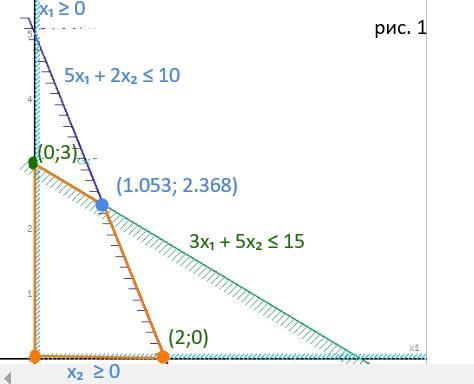
Нам нужно построить область допустимых решений, т.е. надо решить систему уравнений графически.
В системе у ас заданы уравнения прямых.
Каждую прямую строим по двум точкам (я уже не буду подробно расписывать точки - это элементарные действия. )
Для каждой прямой мы определим полуплоскость, которая задается неравенством.
У нас будет 4 прямых, значит 4 полуплскости.
И вот, та область, которая входит во все полуплоскости и будет областью допустимых значений.
Прямые, полуплоскости и рбласть допустимых решений изображены на рис. 1.
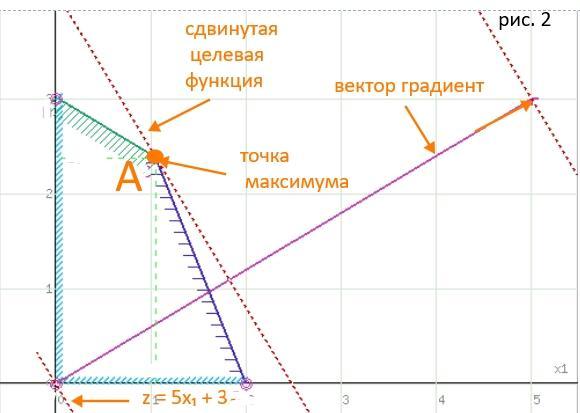
Теперь будем возиться с целевой функцией.
z = 5x₁ + 3x₂ → max.
Cтроим график 5x₁ + 3x₂ = 0.
Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации z.
Начало вектора – точка (0; 0),
конец – точка (5;3).
И нам надо "двигать" эту прямую параллельным образом по направлению, которое определяет вектор градиент. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области.
Это будет точка А.
Этот этап отображен на рис. 2.
Найдем теперь х₁ и х₂ для этой точки.
Для этого решим систему неравенств
из второго выразим х₂ = 5 - 2,5х₁
Подставим в первое
3х₁ + 5(5 - 2,5х₁) = 15
- 9,5х₁ = -10
х₁ ≈ 1,053
х₂ ≈ 2,3684
Теперь подставим эти значения в целевую функцию и получим, что максимум целевой функции равен
z = 5* 1,053 + 3*2,3684 ≈ 12,3684
Примечание: если нужно точное решение, надо систему решить в смешанных числах и получить все в дробях....
но у меня уже а это нет сил....