Предмет: Математика,
автор: Reideen
Задание приложено...
Приложения:
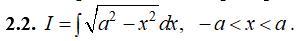
Ответы
Автор ответа:
1
Ответ:
Примечание:
Формула понижения степени:
По таблице интегралов:
По свойствам интегралов:
Пошаговое объяснение:
2.2
----------------------------------------------------------------------------------------------------------
Замена:
----------------------------------------------------------------------------------------------------------
Похожие вопросы
Предмет: Русский язык,
автор: Kik228391
Предмет: Қазақ тiлi,
автор: asiya87
Предмет: Русский язык,
автор: airat781
Предмет: Математика,
автор: darya140704
Предмет: Другие предметы,
автор: evgeniyarybalko0209