Question

ОЧЕНЬ СРОЧНО ПРОШУ! 20 БАЛЛОВ
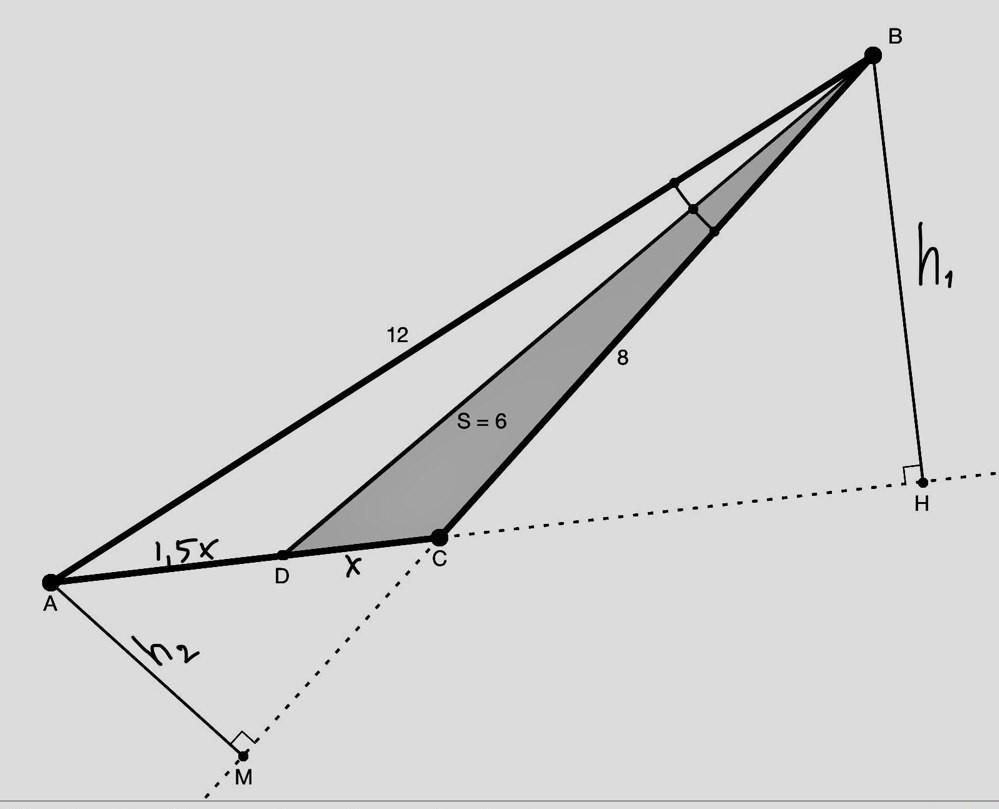
В треугольнике ABC,BD-биссектриса,АМ-высота.АВ=12см,ВС=8см и площадь треугольника BDC=6.Найдите АМ

Answer 1

Ответ:

АМ = 3,75 см

Пошаговое объяснение:

Дано: ∆АВС,

АМ - высота, АМ_|_ВС

ВD - биссектриса, уг.ABD = уг.CBD

АВ=12см, ВС=8см, S(∆BDC) = 6

Найти: АМ = ?

Решение. Построим чертеж, учитывая все, что известно (см рис.).

Доп-но проведем высоту СН,

СН_|_АВ (см. рис.). Обозначим ее h1

Рассмотрим ∆АВС.

BD - биссектриса => она делит противолежащую сторону на части пропорционально длинам боковых сторон:

$\frac{BA}{DA} =\frac{BC}{DC} \: \: { < = > } \: \: \:\frac{BA}{BC} =\frac{DA}{DC} \\ \\ \small BA{ =} 12; \: BC{ =} 8 \: = > \:\frac{BA}{BC} {= }\frac{12}{8} { = }1.5 \: \:{ = > } \\ { = > } \: \: \frac{DA}{DC} {=} \frac{BA}{BC} {=} 1.5 \: \: { = > } \\ { = > }\: {DA} = 1.5{DC}$

DC = x => DA = 1,5x =>

=> AC = AD + DC = 2,5x

Соответственно, площади каждого из ∆-ков можно вычислять как половину произведения его стороны на опущенную к ней высоту.

Найдем площадь "большого" треугольника АВС

через площади треугольников BAD и BDC:

$S_{\triangle BDC} =\frac {1}{2}\cdot DC\cdot h_1 = 6\\ \small S_{\triangle BAD} = \frac {1}{2}\cdot DA\cdot h_1 = \frac {1}{2}\cdot1.5 \cdot DC\cdot h_1 = \\ = 1.5 \cdot S_{\triangle BAD} = 1.5 \cdot6 = 9 \\ \\ S_{\triangle ABC} = S_{\triangle BAD}{ +}S_{\triangle BDC} = 9{ + }6 = 15$

Однако площадь треугольника АВС также вычисляется по той же формуле но относительно другой стороны BC и высоты АМ, которую нам и надо найти.

Обозначим искомую длину АМ = h2. Тогда:

$S_{\triangle ABC} {=} \frac {1}{2}\cdot BC\cdot h_2 \: \: {< = > } \: \: h_2 =\frac{2 S_{\triangle ABC} }{BC} \\ S_{\triangle ABC} =15;\; BC=8 => \\=> \;\,h_2 = \frac{2 \cdot15}{8} = \frac{30}{8} = \frac{15}{4} = 3.75$

А значит,

$AM = h_2 = 3.75 \: \: cm$

Это и будет ответ.