Предмет: Математика,
автор: xvvsain
Интеграл...............
Приложения:
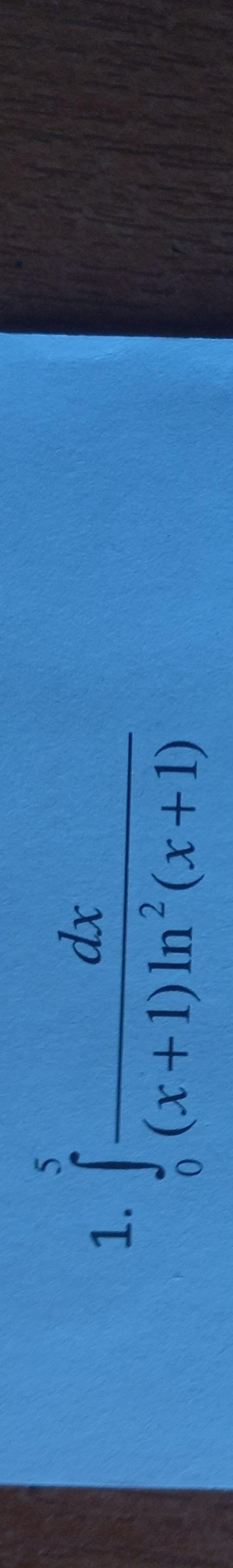
Ответы
Автор ответа:
4
Решение.
Подынтегральная функция разрывна на промежутке [0;5] , так как
при х=0 имеем , и знаменатель дроби
обращается в ноль , функция не определена при х=0 . Значит имеем
несобственный интеграл 2 рода .
Похожие вопросы
Предмет: Русский язык,
автор: Ulchik666
Предмет: Русский язык,
автор: Помогающий203
Предмет: Русский язык,
автор: АндрейМинер
Предмет: Физика,
автор: 89531267895
Предмет: Українська мова,
автор: rtetrdgggdrtgr2332