Предмет: Алгебра,
автор: Alexxx0013
Решить методом исключения систему линейных неоднородных дифференциальных уравнений
Приложения:
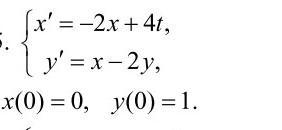
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Выразим из второго уравнения x через y: x=y'+2y⇒x'=y''+2y' и подставим в первое уравнение:
y''+2y'=-2y'-4y+4t; y''+4y'+4y=4t.
Получили линейное неоднородное дифференциальное уравнение с постоячнными коэффициентами. Решим сначала соответствующее однородное уравнение с помощью характеристического уравнения:
Поскольку правая часть неоднородного уравнения является квазимногочленом, частное решение можно искать с помощью неопределенных коэффициентов:
Подставив в уравнение, получаем
откуда общее решение
Отсюда
Остается воспользоваться начальными условиями:
Получаем
Alexxx0013:
спасибо большое
Похожие вопросы
Предмет: Английский язык,
автор: орпоп
Предмет: Английский язык,
автор: соня1190
Предмет: Русский язык,
автор: людмила207
Предмет: Математика,
автор: alexoo9o
Предмет: Химия,
автор: sabrinaaaa31