Question

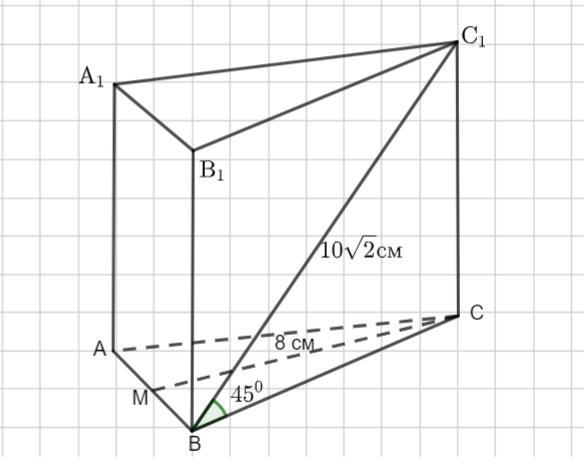
Основа прямої призми рівнобедрений трикутник, у якого висота, проведена до основи дорівнює 8 см. Діагональ бічної грані, яка містить бічну сторону трикутника, дорівнює 10√2 см і утворює з площиною кут 45о . Знайти: а) бічне ребро призми; б) бічну поверхню призми; в) повну поверхню призми.

Answer 1

Ответ:

а) боковое ребро призмы равно 10 см.

б) площадь боковой поверхности призмы равна 320 см²

в) площадь полной поверхности призмы равна 416 см²

Объяснение:

Пусть дана прямая призма $ABCA_{1} B_{1}C_{1}$.

Основание призмы Δ АВС- равнобедренный( АС = ВС) .

СМ - высота, проведенная к основанию АВ, СМ=8 см.

Диагональ боковой грани $BC_{1}=10\sqrt{2}$ cм и образует $\angle{}C_{1} BC =45^{0} .$

Надо найти:

а) боковое ребро призмы;

б) боковую поверхность призмы;

в) площадь полной поверхности призмы.

а) Так как призма прямая, то Δ $C_{1} CB-$ прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

Тогда, если  $\angle{}C_{1} BC =45^{0} ,$ то $\angle{}BC_{1} C =90^{}- 45^{0}=45^{0} .$

Если в треугольнике два угла равны, то он равнобедренный и $BC= CC_{1}$

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе

$sin\angle{}C_{1} BC =\dfrac{CC_{1} }{BC_{1} } ;\\\\sin 45^{0} =\dfrac{CC_{1} }{10\sqrt{2} } ;\\\\\dfrac{\sqrt{2} }{2} =\dfrac{CC_{1} }{10\sqrt{2} };\\\\CC_{1} =\dfrac{10\sqrt{2} \cdot \sqrt{2} }{2} =10$

$BC= CC_{1}=10$ см.

Значит, боковое ребро призмы равно 10 см.

б) Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.

Найдем периметр равнобедренного треугольника АВС.

Рассмотрим ΔСМВ - прямоугольный, так как по условию СМ - высота, проведенная к основанию. СМ - медиана и биссектриса.

По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$BC^{2} =CM^{2} +MB^{2} ;\\MB^{2} =BC^{2} -CM^{2};\\MB= \sqrt{BC^{2} -CM^{2}};\\MB=\sqrt{10^{2}-8^{2} } =\sqrt{100-64} =\sqrt{36} =6$ см.

Тогда $AB= 2\cdot 6 =12$ cм

$P= AB+BC+AC ;\\P= 12+10+10=32$ cм

Высота призмы равна длине бокового ребра, то есть 10 см

Тогда площадь боковой поверхности призмы будет

$S= P\cdot H;\\P= 32\cdot 10 =320$ см²

в) найдем площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить удвоенную площадь основания.

Найдем площадь треугольника как полупроизведение стороны на высоту. проведенную к этой стороне

$S= \dfrac{1}{2} \cdot AB\cdot CM;\\\\S= \dfrac{1}{2} \cdot 12\cdot 8=6\cdot8=48$

Значит, площадь основания призмы равна 48 см².

Тогда площадь полной поверхности:

$S =320+2\cdot 48=320+96= 416$ см²

#SPJ1