СРОЧНО!!!!!!!!
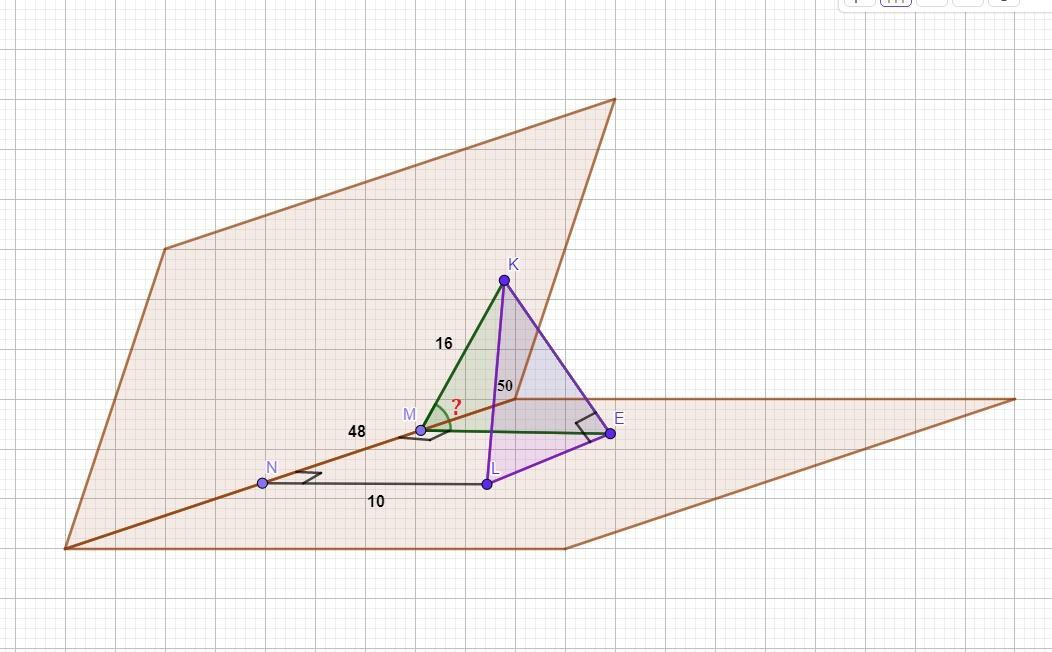
Из точек M и N ребра двугранного угла в разных его гранях возведены перпендикуляры MK и NL. Определите величину двугранного угла,учитывая, что MN -48 см MK-16 см Nl-10 см расстояние между точками K и L равно 50 см.
Ответы
Ответ:
Величина двугранного угла равна 60°
Объяснение:
Из точек M и N ребра двугранного угла в разных его гранях возведены перпендикуляры MK и NL. MN =48 см MK=16 см NL=10 см KL=50 см. Нужно определить величину двугранного угла.
- Величиной двугранного угла называется величина его линейного угла.
Проведём отрезок МЕ║NL и равный NL. МЕ=NL = 10 см.
- Если две противоположные стороны четырехугольника равны и параллельны, то такой четырехугольник параллелограмм.
⇒NMEL - параллелограмм.
Так как MK⊥MN, NL⊥MN, то NMEL - прямоугольник.
- Прямоугольник - это параллелограмм, у которого все углы прямые.
Так как у прямоугольника противоположные стороны равны, то LE=MN=48 cм
МЕ⊥MN, MK⊥MN, то ∠КМЕ - линейный угол двугранного угла.
Найдём ∠КМЕ.
MN⊥ME, MN⊥MK ⇒ MN⊥ плоскости ΔМКЕ, т.к. она перпендикулярна двум пересекающимся прямым в этой плоскости. Следовательно параллельная ей прямая LE тоже перпендикулярна этой плоскости, а значит КЕ⊥LE.
Рассмотрим прямоугольный ΔKEL (∠Е=90°).
По теореме Пифагора найдём катет КЕ:
KE²=KL²-LE²=50²-48²=2500-2304=196
KE=√196=14 см
Рассмотрим ΔКМЕ.
В нем известны все стороны: КМ = 16 см, МЕ = 10 см, КЕ = 14 см.
По теореме косинусов найдём угол КМЕ:
КЕ²=КМ²+МЕ²-2*КМ*МЕ*cos∠КМЕ
16²+10²-2*16*10*cos∠КМЕ=14²
-320*cos∠КМЕ=196-256-100
cos∠КМЕ = -160/-320
cos∠КМЕ=1/2
∠КМЕ = 60°
#SPJ1