Question

Докажите, что середины выпуклого четырехугольника являются вершинами параллелограмма.

Answer 1

Ответ:

Объяснение:

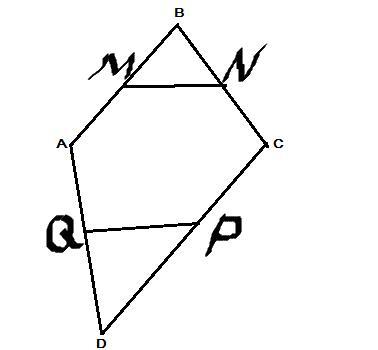
 Скористаємось наявним рисунком . Проведемо діагоналі AC  i BD

  опуклого 4 - кутника ABCD .Тоді відрізок MN є середньою лінією

   ΔАВС , а відрізок  QP є середньою лінією  ΔАDС .

   Тому : 1) MN║AC  i  QP║AC . На основі транзитивної властивості

   паралельності прямих  MN║QP .

              2) MN = 1/2 AC  i  QP =  1/2 AC , тому MN = QP .

   Отже , в  4 - кутнику  MNPQ  дві протилежні сторони паралельні

    і  рівні , тому , як відомо , він є паралелограмом . Доведено .

     

Answer 2

Ответ:

Предположим, что точки M, N, P, Q выпуклого четырехугольника ABCD являются серединами сторон AB, BC, CD, AD

проведем диагональ АС

MN  является средней линией треугольника ABC,

значит MN║AC и равен ее половине

средней линией треугольника ADC является PQ

значит  PQ║MN и равен ее половине

вообщем получается что PQ║MN

                                             PQ=MN

Две стороны четырехугольника параллельны и равны друг другу, что доказывает, что четырехугольник является параллелограммом.