Question

Обчислити площу фігури, що обмежена лініями:
ух=3, у=3 і х=3

Answer 1

Ответ:

Площадь фигуры равна $3\dfrac{1}{3}$  кв. ед.

Пошаговое объяснение:

Вычислить площадь фигуру, ограниченную линиями

$yx=3,y=3,x=3$

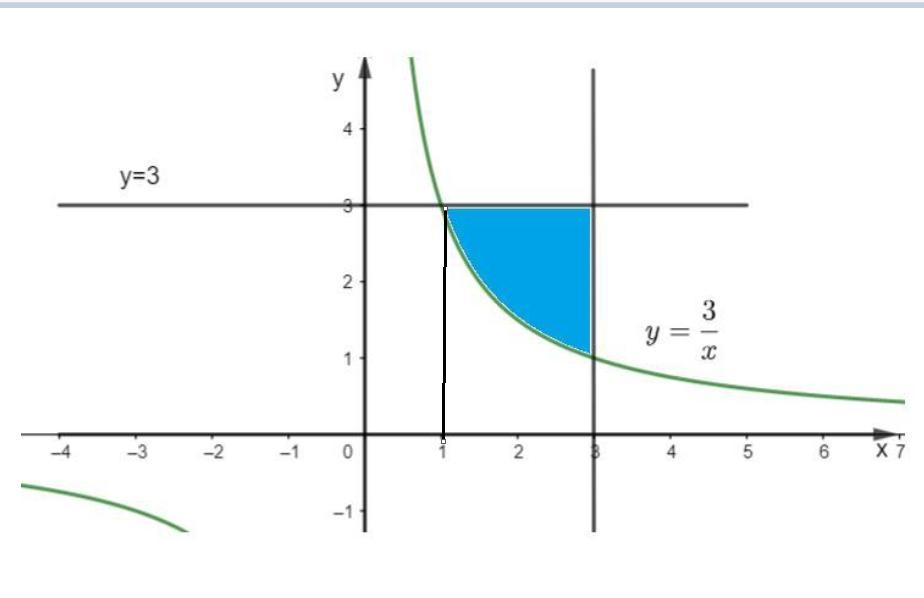
Выполним рисунок

$yx=3;\\\\y=\dfrac{3}{x}$

Данная функция является обратной пропорциональностью и графиком данной функции является гипербола, ветви которой расположены в первой и третьей четвертях.

Графиком $y=3$ является прямая, параллельная оси абсцисс и проходящая через точку (0; 3)

Графиком $x=3$ является прямая, параллельная оси ординат и проходящая через точку (3; 0)

Найдем абсциссу точки пересечения графика функции  $y=\dfrac{3}{x}$  и

$y=3$ , решив уравнение:

$\dfrac{3}{x}=3|\cdot x\neq 0;\\\\3=3x;\\x=3:3;\\x=1$

Рисунок во вложении. Фигура, площадь которой надо определить выделена голубым цветом. Эта фигура не является криволинейной трапецией, поэтому площадь фигуры найдем

$S= \int \limits ^3_1 {(f{_1}(x)- f{_2}(x))} \, dx$

$f{_1}(x) = 3;\\\\f{_2}(x) =\dfrac{3}{x}$

$S= \int\limits^3_1 {\left(3-\dfrac{3}{x} \right)} \, dx =\left(3x+\dfrac{3}{x^{2} }\right ) \bigg|^3_1 =\left(3\cdot3+\dfrac{3}{3^{2} }\right )-\left(3\cdot1 +\dfrac{3}{1^{2} } \right)=\\\\=9+\dfrac{3}{9} -3-3=3+\dfrac{1}{3} =3\dfrac{1}{3}$

Значит, площадь фигуры равна $3\dfrac{1}{3}$  кв. ед.

#SPJ1