Question

Вычислите площадь фигуры ограниченной линиями у=6х2 и у=18х срочно пожалуюста

Answer 1

Ответ:

Площадь фигуры ограниченной линиями у = 6х² и у = 18х равна 27 ед.²

Объяснение:

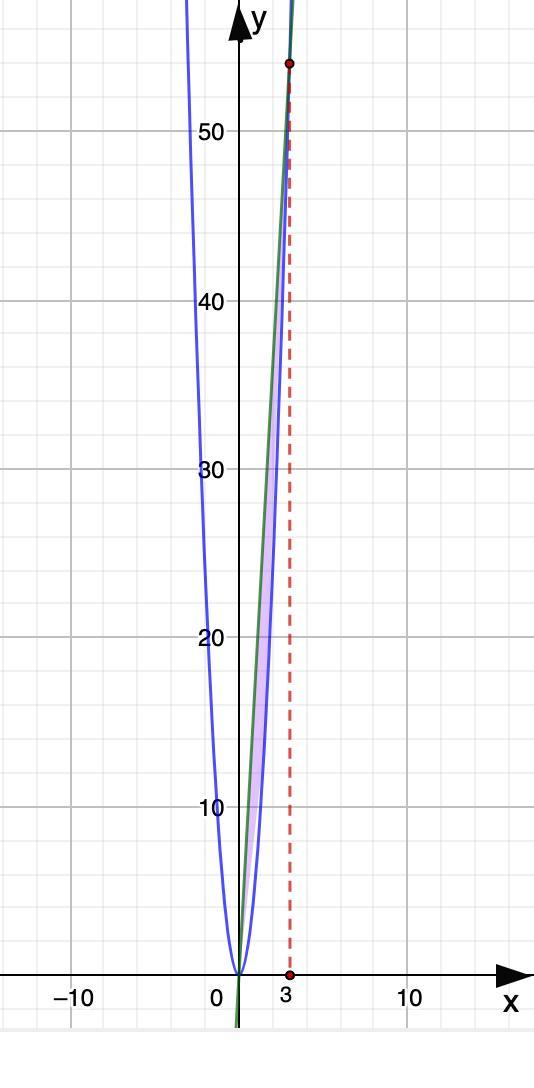
Вычислите площадь фигуры ограниченной линиями у = 6х² и у = 18х.

Построим графики и определим искомую площадь.

1) y = 6x²

- квадратичная функция, график - парабола.

Ветви вверх, симметрична относительно оси Оу.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c| }\cline{1-4}x& 0 & 1 & 2 \\\cline{1-4}y& 0 & 6 & 24 \\\cline{1-4}\end{array}$

Вторая ветвь симметрична оси Оу.

2. у = 18х

-линейная функция, график - прямая.

Для построения достаточно двух точек.

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c| }\cline{1-3}x& 1 & 2 \\\cline{1-3}y& 1 8& 36 \\\cline{1-3}\end{array}$

Найдем точки пересечения параболы и прямой, решив систему уравнений:

$\displaystyle \left \{ {{y=6x^2} \atop {y=18x}} \right. \\\\6x^2 = 18x\\\\6x(x-3) = 0\\\\x = 0;\;\;\;\;\;x=3$

Воспользуемся формулой для нахождения площади фигуры:

$\displaystyle \boxed { S = \int\limits^b_a {(f_2(x)-f_1(x))} \, dx }$

У нас b = 3; a = 0.

f₂(x) = 18x;   f₁(x) = 6x²

Найдем площадь:

$\displaystyle \int\limits^3_0 {(18x-6x^2)} \, dx =\left(\frac{18x^2}{2}-\frac{6x^3}{3}\right)\bigg|^3_0=\\ \\ =(9x^2-2x^3)\big|^3_0$

Теперь нам понадобится формула Ньютона-Лейбница:

$\boxed {\int\limits^b_a {f(x)} \, dx=F(b)-F(a) }$

Получим:

$(9x^2-2x^3)\big|^3_0=9\cdot9-2\cdot27-0=27$

Площадь фигуры ограниченной линиями у = 6х² и у = 18х равна 27 ед.²

#SPJ1