Предмет: Математика,
автор: Tgggghjgxsdthjkkfdhj
ДАЮ 20 БАЛЛОВ ОЧЕНЬ СРОЧНО
В треугольнике ABC,угол А=90,О-точка пересечения медиан.Ок=5,ОМ=2корней из 10,найдите площадь треугольника АОС.
рисунок 2.38.
Приложения:
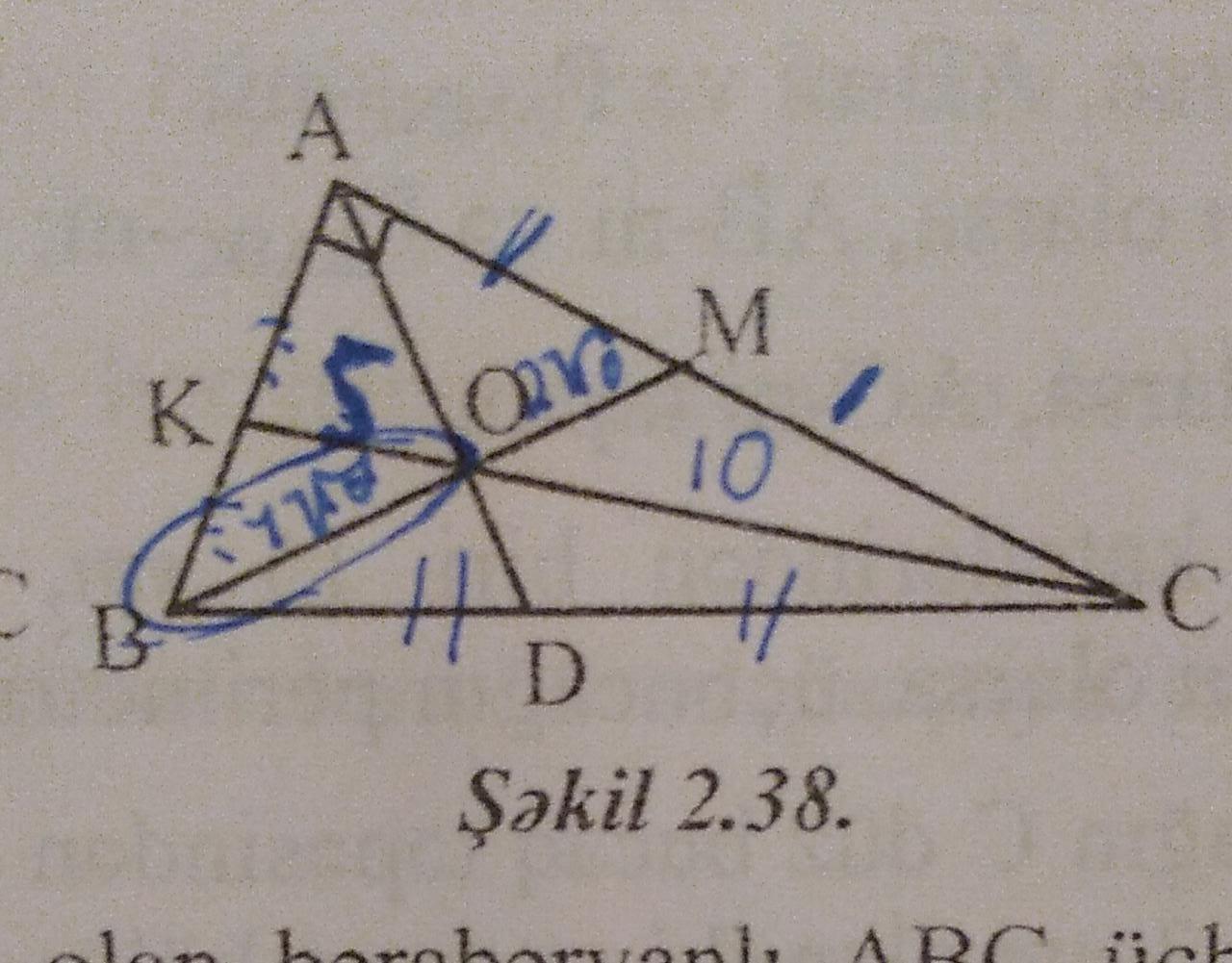
Ответы
Автор ответа:
1
Ответ:
S∆ABC = 1/2∙AB∙AC = 1/2∙18∙12 = 108
Пошаговое объяснение:
CK = 3∙OK = 3∙5 = 15
BM = 3∙OM = 3∙2√10 = 6√10
Пусть AM = x, тогда AC = 2x.
Пусть AK = y, тогда AB = 2y.
Составим теорему Пифагора для ∆CAK и ∆MAB:
(2x)^2 + y^2 = 15^2
x^2 + (2y)^2 = (6√10)^2
4x^2 + y^2 = 225
x^2 + 4y^2 = 360
y^2 = 225 - 4x^2
x^2 + 4(225 - 4x^2) = 360
x^2 + 4(225 - 4x^2) = 360
x^2 + 900 - 16x^2 = 360
540 = 15x^2
x = 6
y^2 = 225 - 4∙6^2
y^2 = 225 - 144
y = 9
AC = 2∙6 = 12
AB = 2∙9 = 18
S∆ABC = 1/2∙AB∙AC = 1/2∙18∙12 = 108
S∆ABC = 1/2∙AB∙AC = 1/2∙18∙12 = 108
Пошаговое объяснение:
CK = 3∙OK = 3∙5 = 15
BM = 3∙OM = 3∙2√10 = 6√10
Пусть AM = x, тогда AC = 2x.
Пусть AK = y, тогда AB = 2y.
Составим теорему Пифагора для ∆CAK и ∆MAB:
(2x)^2 + y^2 = 15^2
x^2 + (2y)^2 = (6√10)^2
4x^2 + y^2 = 225
x^2 + 4y^2 = 360
y^2 = 225 - 4x^2
x^2 + 4(225 - 4x^2) = 360
x^2 + 4(225 - 4x^2) = 360
x^2 + 900 - 16x^2 = 360
540 = 15x^2
x = 6
y^2 = 225 - 4∙6^2
y^2 = 225 - 144
y = 9
AC = 2∙6 = 12
AB = 2∙9 = 18
S∆ABC = 1/2∙AB∙AC = 1/2∙18∙12 = 108
flsh:
Произошёл сбой со связью. Не могу довести решение до конца
так вы нашли чему равен площадь AВС,а площадь АОС?
равна*
SΔAOC = 2/3 * 1/2 * SΔABC = 1/3 * 108 = 36
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: pavlenkodiana39
Предмет: Английский язык,
автор: russkayadevushkaa
Предмет: Математика,
автор: lena10081