Question

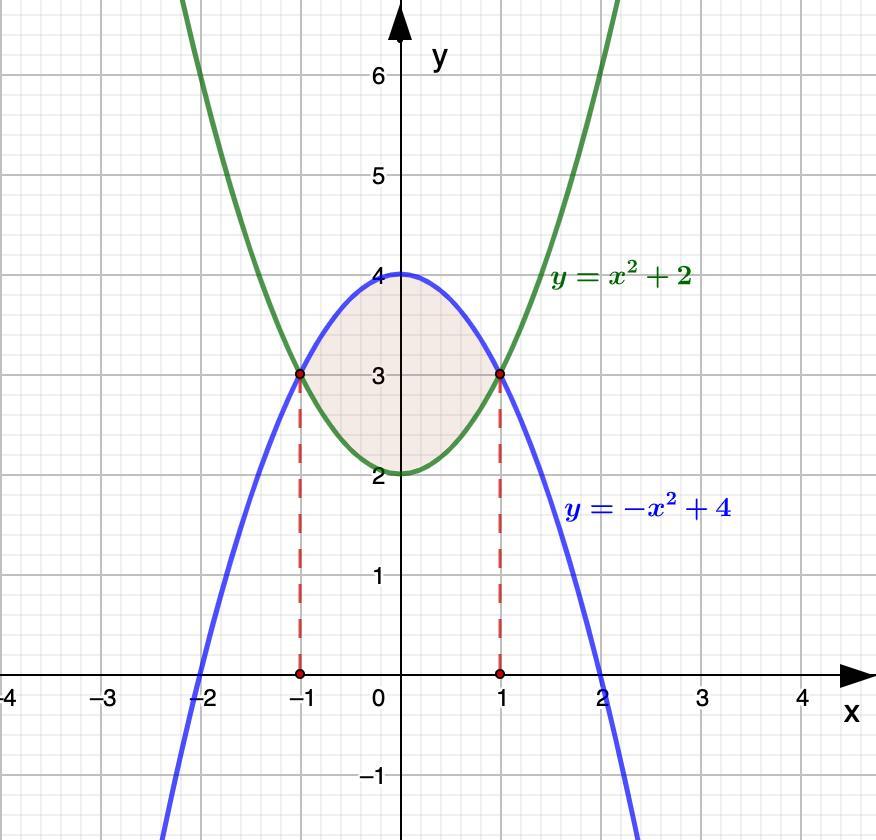
обчислити площу фігури, обмеженою лініями y=x^2+2, y=-x^2+4

Answer 1

Ответ:

Площадь фигуры, ограниченной линиями y=x²+2, y=-x²+4 равна $\displaystyle 2\frac{2}{3}$  ед.²

Объяснение:

Вычислить площадь фигуры, ограниченной линиями y=x²+2, y=-x²+4.

Определим фигуру, площадь которой надо вычислить.

Построим данные графики.

1) у = х² + 2

- квадратичная функция, график - парабола, ветви вверх.

Этот график получается из графика у = х² путем сдвига на две единицы вверх.

2) у = -х² + 4

- квадратичная функция, график - парабола, ветви вниз.

Этот график получается из графика у = -х² путем сдвига на четыре единицы вверх.

Найдем точки пересечения этих графиков.

Решим систему:

$\displaystyle \left \{ {{y=x^2+2} \atop {y=-x^2+4}} \right.$

x² + 2 = -x² + 4

2x² - 2 = 0

2(x - 1)(x + 1) = 0

x₁ = 1;     x₂ = -1

C фигурой определились.

Площадь найдем по формуле:

$\displaystyle \boxed { S = \int\limits^b_a {(f_2(x) - f_1(x))} \, dx }$

Так же нам понадобится формула Ньютона - Лейбница:

$\boxed {\int\limits^b_a {f(x)} \, dx =F(b) - F(a)}$

У нас:  a = -1; b = 1; f₁(x) = -x² + 4; f₂(x) = x₂ + 2.

$\displaystyle \int\limits^1_{-1} {(-x^2+4-x^2-2)} \, dx =\\\\\int\limits^1_{-1} {(-2x^2+2)} \, dx =\left(-\frac{2x^3}{3} +2x\right)\bigg|^1_{-1}=\\\\=-\frac{2}{3}+2-\left(\frac{2}{3}-2\right) =-\frac{4}{3}+4=2\frac{2}{3}$

Площадь фигуры, ограниченной линиями y=x²+2, y=-x²+4 равна $\displaystyle 2\frac{2}{3}$  ед.²