Question

Задание приложено...

Answer 1

Ответ:

1) $\boxed{ \boldsymbol{ \displaystyle \iint\limits_{D} {(x - y)} \, dxdy = \frac{2}{3} } }$

2) $\boxed{ \boldsymbol{\displaystyle \iint\limits_{D} {x^{4}y} \, dxdy = \frac{166}{21} }}$

Примечание:

Для задачи 1)

Для вычисления двойного интеграла сведем его к повторному интегралу. Будем интегрировать по y, поэтому приведения в общем

виде к повторному интегралу двойного по области $D$ будет в виде:

$\boxed{ \boldsymbol{ \displaystyle \iint\limits_{D} f(x,y) \, dxdy = \int\limits^a_b \, dy \int\limits^{\xi_{2}(y)}_{\xi_{1}(y)} {f(x,y)} \, dx } }$

При этом функции $\xi_{1} (y), \xi_{2} (y)$ - функции ограничивающие область $D$ слева и справа соответственно.

Для задачи 2)

Для вычисления двойного интеграла сведем его к повторному интегралу. Будем интегрировать по x, поэтому приведения в общем

виде к повторному интегралу двойного по области $D$ будет в виде:

$\boxed{ \boldsymbol{ \displaystyle \iint\limits_{D} f(x,y) \, dxdy = \int\limits^a_b \, dx \int\limits^{\phi_{2}(x)}_{\phi_{1}(x)} {f(x,y)} \, dy } }$

При этом функции $\phi_{1} (x), \phi_{2} (x)$ - функции ограничивающие область $D$   снизу и сверху соответственно.

Объяснение:

1)

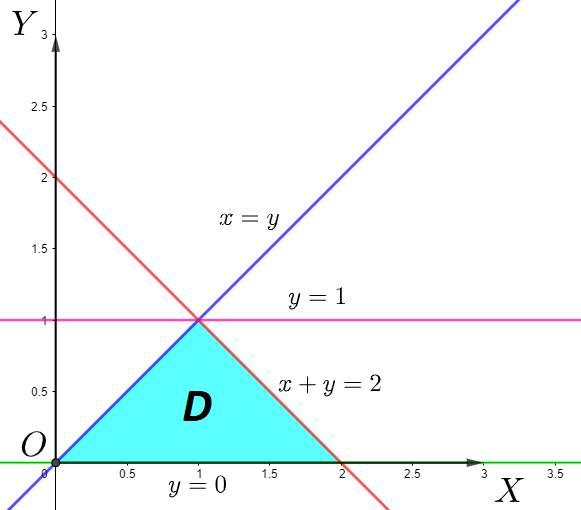
Область (голубая область) $D:$

$y = 0$

$x = y$

$x + y = 2 \Longrightarrow x = 2 - y$

Найдем ординату пересечения графиков $x = y$ и $x = 2 - y:$

$y = 2 - y$

$2y = 2|:2$

$y = 1$

Границы интегрирования: от 0 до 1

----------------------------------------------------------------------------------------------------------

$\displaystyle \iint\limits_{D} {(x - y)} \, dxdy = \int\limits^{1}_{0} \, dy \int\limits^{2- y}_{y} (x - y) \, dx = \int\limits^{1}_{0} \bigg( \bigg(\frac{x^{2}}{2} - yx \bigg) \bigg |^{2 - y}_{y} \bigg) \, dy =$

$\displaystyle = \int\limits^{1}_{0} \bigg( \bigg(\frac{(2 - y)^{2}}{2} - y(2 - y) \bigg) - \bigg(\frac{y^{2}}{2} - y^{2} \bigg) \bigg) \, dy =$

$\displaystyle = \int\limits^{1}_{0} \bigg(\frac{(2 - y)^{2}}{2} - 2y + y^{2} - \frac{y^{2}}{2} + y^{2} \bigg) \, dy =\int\limits^{1}_{0} \bigg(\frac{(2 - y)^{2}}{2} - 2y + \frac{3y^{2}}{2} \bigg) \, dy =$

$\displaystyle = \int\limits^{1}_{0} \bigg(\frac{4 - 4y + y^{2} - 4y + 3y^{2}}{2} \bigg) \, dy = \int\limits^{1}_{0} \bigg(\frac{4 - 8y + 4y^{2}}{2} \bigg) \, dy =$

$= \displaystyle 2 \int\limits^{1}_{0} \bigg(y^{2} - 2y + 1 \bigg) \, dy =2 \int\limits^{1}_{0} \bigg(y - 1 \bigg)^{2} \, d(y - 1)= 2\bigg( \bigg( \frac{(y - 1)^{3}}{3} \bigg)\bigg|^{1}_{0} \bigg) =$

$\displaystyle = 2\bigg( \bigg( \frac{(1 - 1)^{3}}{3} \bigg) - \bigg( \frac{(0 - 1)^{3}}{3} \bigg)\bigg) = 2 \bigg(0 - \bigg(-\frac{1}{3} \bigg) \bigg) = \frac{2}{3}$

2)

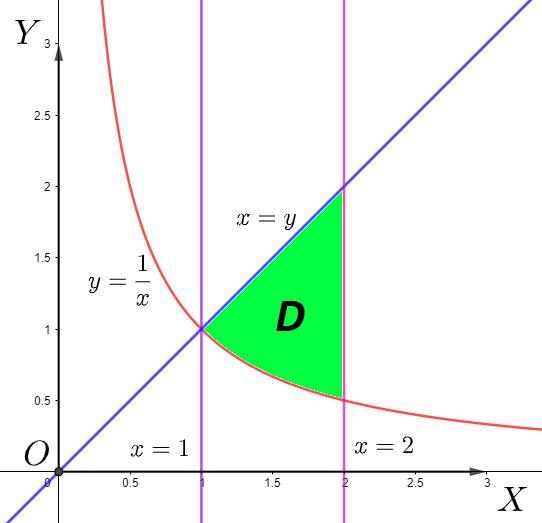
Область (зеленая область) $D:$

$xy = 1 \Longrightarrow y = \dfrac{1}{x}$

$x = y$

$x = 2$

Найдем абсциссу пересечения графиков $y = x$ и $y = \dfrac{1}{x} :$

$x = \dfrac{1}{x} \Longleftrightarrow x^{2} = 1$ (x = 0, не является корнем данного уравнения)

$x_{1,2} = \pm 1 \Longrightarrow x = 1$, так как прямая y = 0 является асимптотой графика $y = \dfrac{1}{x}$, то часть графика лежащая ниже оси OX не будет иметь общих точек с прямой x = 2)

Границы интегрирования: от 1 до 2

----------------------------------------------------------------------------------------------------------

$\displaystyle \iint\limits_{D} {x^{4}y} \, dxdy = \int\limits^{2}_{1} \, dx \int\limits^{x}_{ \frac{1}{x} } x^{4}y \, dy = \int\limits^{2}_{1} x^{4} \Bigg( \bigg( \frac{y^{2}}{2} \bigg) \bigg |^{x}_{ \frac{1}{x} } \Bigg) \, dx =$

$\displaystyle = \frac{1}{2} \int\limits^{2}_{1} x^{4} \Bigg( \bigg( y^{2} \bigg) \bigg |^{x}_{ \frac{1}{x} } \Bigg) \, dx = \frac{1}{2} \int\limits^{2}_{1} x^{4} \bigg( x^{2} - \frac{1}{x^{2} } \bigg) \, dx = \frac{1}{2} \int\limits^{2}_{1} \bigg( x^{6} - x^{2} \bigg) \, dx =$

$\displaystyle = \frac{1}{2} \Bigg( \bigg(\frac{x^{7}}{7}- \frac{x^{3}}{3} \bigg) \bigg |^{2}_{1} \Bigg)= \frac{1}{2} \Bigg( \bigg(\frac{2^{7}}{7}- \frac{2^{3}}{3} \bigg) - \bigg(\frac{1^{7}}{7}- \frac{1^{3}}{3} \bigg) \Bigg) =$

$\displaystyle = \frac{1}{2} \Bigg( \bigg(\frac{128}{7}- \frac{8}{3} \bigg) - \bigg(\frac{1}{7}- \frac{1}{3} \bigg) \Bigg) = \frac{1}{2} \Bigg( \frac{128}{7}- \frac{8}{3} - \frac{1}{7}+ \frac{1}{3} \Bigg) = \frac{1}{2} \Bigg(\frac{127}{7} -\frac{7}{3} \Bigg)=$

$\displaystyle = \frac{1}{2} \Bigg(\frac{381 - 49}{21} \Bigg)= \frac{332}{2 \cdot 21} = \frac{166}{21}$