Решить ОДИН интеграл. 100 баллов.
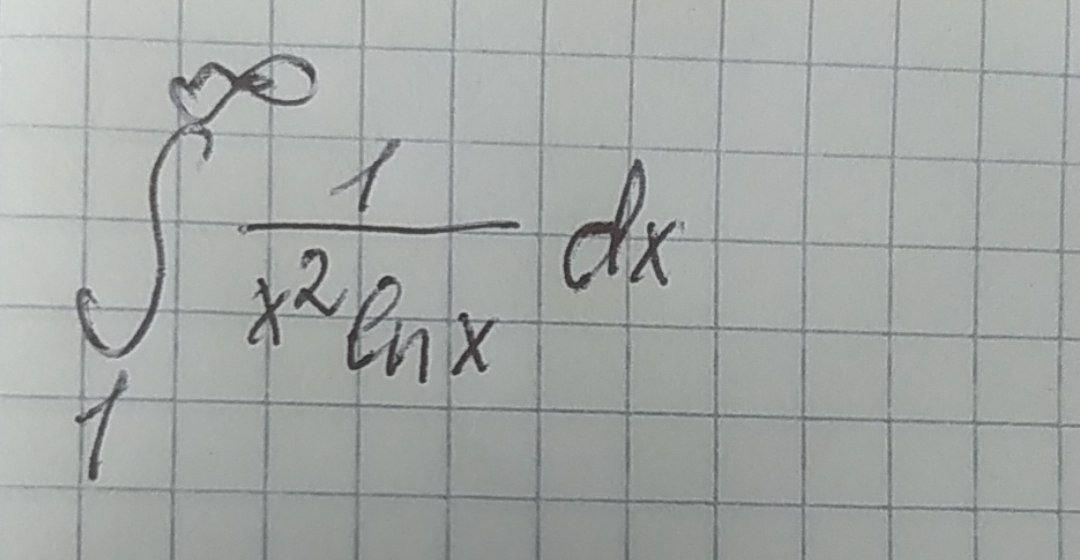
Ответы
Ответ:
расходится
Пошаговое объяснение:
Докажем расходимость этого интеграла. Во-первых, заметим, что функция положительна, поэтому можно пользоваться признаками сходимости. Поскольку у нас две проблемные точки - бесконечность и 1, теория рекомендует разбить интеграл на два, скажем, от 1 до e и от e до бесконечности.
На бесконечности интеграл сходится, поскольку подинтегральная функция меньше а интеграл от
при p>1 на бесконечности сходится (для тех кто не в курсе - при интегрировании степенной функции показатель увеличивается на 1, поэтому икс остается в знаменателе, и при подстановке бесконечности дает ноль (для поборников математической строгости - предел на бесконечности равен нулю))
На самом деле предыдущий абзац спокойно можно было бы опустить, поскольку первый интеграл, как мы сейчас докажем, расходится, а это гарантирует расходимость всего интеграла.
Для облегчения восприятия сделаем в первом интеграле замену переменной: x-1=t; x=t+1; получаем интеграл
Имеем:
при t→0.
Интеграл от последней функции расходится в нуле, поскольку числовой множитель не влияет на сходимость или расходимость, а интеграл от расходится в нуле при p≥ 1 (объяснение: при p>1 после интегрирования t останется в знаменателе и при подстановке нуля даст бесконечность, а при p=1 получаем логарифм, стремящийся к бесконечности, когда аргумент стремится к нулю; впрочем, только этот случай нас и интересует). По признаку сравнения в предельной форме это гарантирует расходимость интеграла от средней функции, а тогда первый признак сходимости дает расходимость интеграла от левой функции.