Предмет: Математика,
автор: TheScoreTop
Решить интеграл⠀⠀⠀⠀⠀⠀⠀
Приложения:
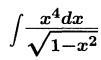
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
Задание выполнено!
Похожие вопросы
Предмет: Русский язык,
автор: aveselova806
Предмет: Русский язык,
автор: vilokcom30
Предмет: Русский язык,
автор: Аноним
Предмет: ОБЖ,
автор: Ulyana766
Предмет: Биология,
автор: Sonyah04