Question

СРОЧНО ПОМОГИТЕ ДАЮ 80 ОЧКОВ!!!!!!!!
прямая, проходящая через начало координат, пересекает окружность x^2+y^2=25 вточке с положительной абсциссой и ординатой -3. Найдите уравнение этой прямой

Answer 1

Ответ:

у = -0,75х

Объяснение:

x²+y²=25 - уравнение окружности с центром в начале координат и радиусом 5
Ордината - это ось у
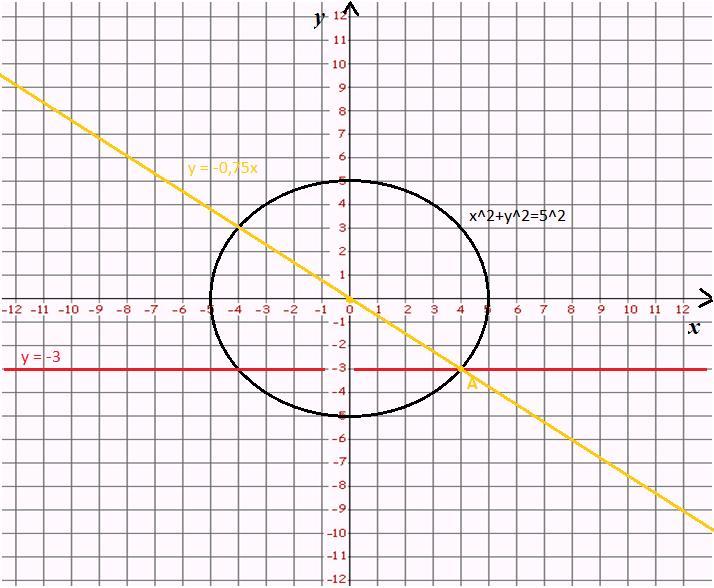
Начертим прямую у = -3 и окружность x²+y²=25(см. вложение)
Графики пересекаются в точках (-4;-3) и (4;-3). Т.к. в условии указано, что абсцисса(ось х) положительна, следовательно искомая точка - это (4;-3). Обозначим её как А.
Уравнение прямой в общем виде выглядит как y = kx+b, где k и b - коэффициенты.
Составим систему для их нахождения, где в 1 уравнении системы подставим координаты начала(0:0), а во втором - точку А:
$\displaystyle \left \{ {{0=k*0+b} \atop {-3=k*4+b}} \right. < = > \left \{ {{b=0} \atop {-3=4k}} \right. < = > \left \{ {{b=0} \atop {k=-0,75}} \right.$
Получается, что уравнение прямой выглядит как у = -0,75х