Предмет: Математика,
автор: illiakutsenko
Помогите пожалуйста решить двойной интеграл
Приложения:

Ответы
Автор ответа:
1
Ответ:
Данный двойной интеграл равен
Пошаговое объяснение:
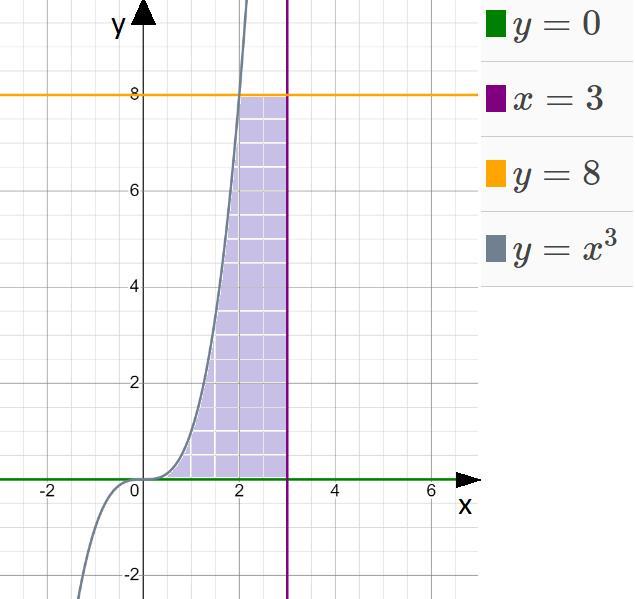
Нарисуем графики на одной плоскости(см. вложение)
Из рисунка видно, что площадь искомой фигуры(закрашена фиолетовым) изменяется 2 раза следующим образом:
а) 0≤x≤2 и 0≤y≤x³
б) 2≤x≤3 и 0≤y≤8
Также можно решить через dydx и один интеграл. Тогда двойной интеграл будет выглядеть как:
Конечный результат будет тем же
Приложения:
illiakutsenko:
Спасибо большое , очень благодарен!
Похожие вопросы
Предмет: Русский язык,
автор: NekoName2007
Предмет: Қазақ тiлi,
автор: лагг
Предмет: Английский язык,
автор: алина122006
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: gubinaleshka