Предмет: Математика,
автор: vsepovzlomu
Помогите срочно
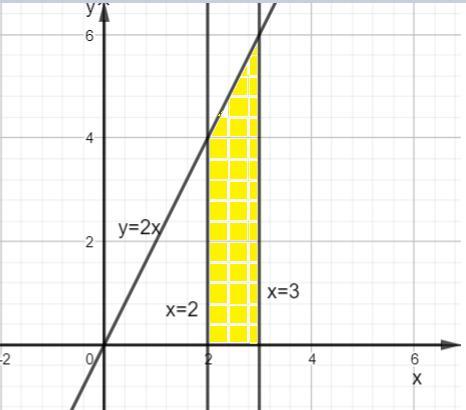
Обчислити площу криволінійної трапеції, обмеженою графіком функції y=2х та прямими х=2, х=3.
Решите пожалуйста
Ответы
Автор ответа:
1
Ответ:
площадь полученной фигуры равна 5 кв. ед
Пошаговое объяснение:
Найти площадь криволинейной трапеции, ограниченной графиком функции y=2x и прямыми х=2 и х= 3 .
Выполним рисунок. Графиком функции y=2x является прямая, проходящая через начало координат и точку (2; 4).
Прямые х=2 и х= 3 - параллельны оси ординат и проходящие соответственно первая через точку (2; 0) и вторая (3; 0) .
Если это криволинейная трапеция, то снизу она ограниченна осью абсцисс. Рисунок во вложении.
Тогда площадь полученной фигуры определяется
Тогда площадь полученной фигуры равна 5 кв. ед
Площадь полученной фигуры можно найти, как площадь трапеции с основаниями 4 и 6 и высотой равной 1 по формуле:
где
a,b- основания трапеции, h- высота трапеции.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sooffu10pluy
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: АбырвалгБулгаков
Предмет: География,
автор: lewchenkoaniut