Question

Відрізок CD-
висота прямокутного трикутника ABC
(<C = 90°). Відрізок СК - бісектриса трикутника ВCD.
Доведіть, що трикутник АСК рівнобедрений
СРООООЧНОООО!​

Answer 1

Ответ:

Доказано, что ΔАСК - равнобедренный.

Объяснение:

Отрезок CD - высота прямоугольного треугольника ABC

(∠C = 90°). Отрезок СК - биссектриса треугольника ВCD.

Доказать, что треугольник АСК равнобедренный.

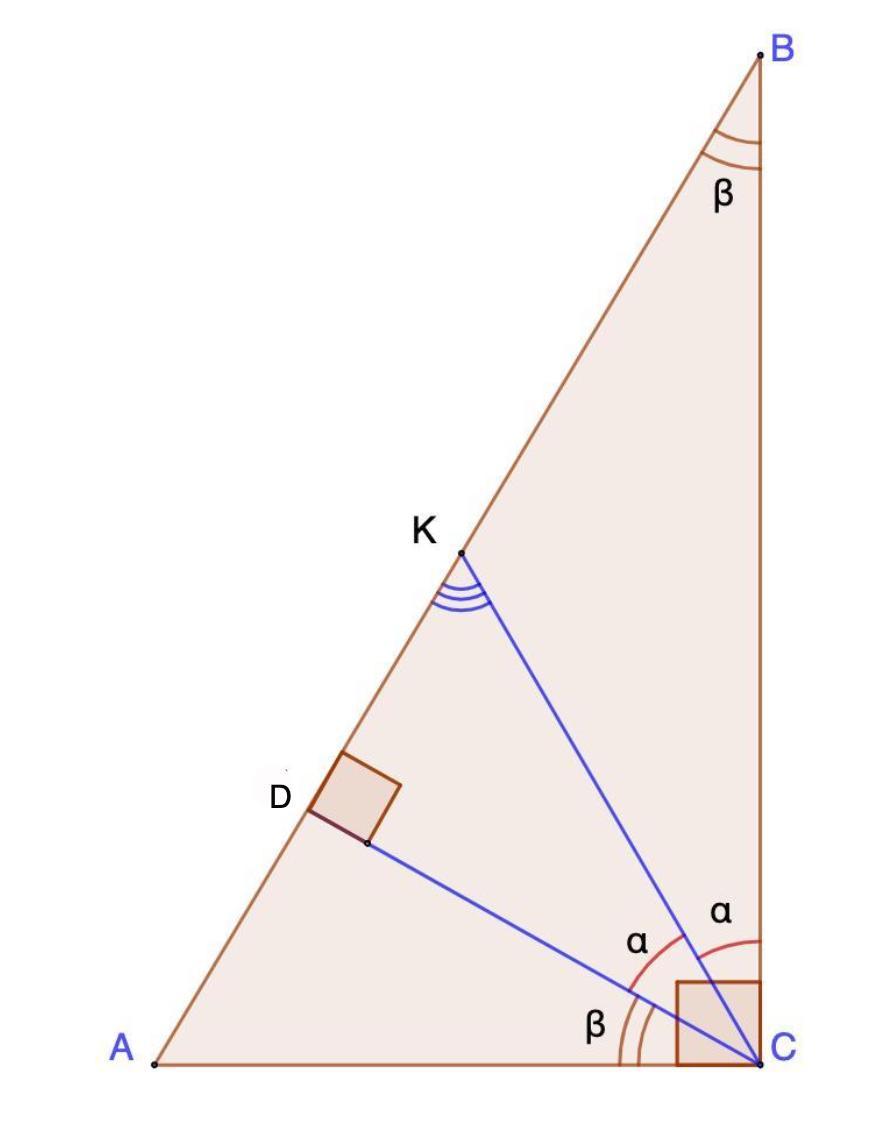
Дано: ΔАВС - прямоугольный;

∠С = 90°;

CD - высота ΔАВС;

СК - биссектриса ∠DCB;

Доказать: ΔАСК - равнобедренный.

Доказательство:

1. Разберемся с углами.

∠DСК = ∠КСВ (СК - биссектриса ∠DCB)

Пусть ∠DСК = ∠КСВ = α;

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ из ΔАВС - прямоугольного:

∠В = 90° - ∠А

из ΔАDС - прямоугольного:

∠АСD = 90° - ∠А

⇒ ∠В = ∠АСD

Пусть ∠В = ∠АСD = β.

2. Рассмотрим ΔАСК.

∠АСК = α + β

• Внешний угол равен сумме двух углов, не смежных с ним.

⇒ ∠АКС = α + β

• Если в треугольнике два угла равны, то он равнобедренный.

⇒ ΔАСК - равнобедренный.

#SPJ1