Предмет: Алгебра,
автор: vasylua6
розв'яжіть рівняння:
а)

б)

Приложения:
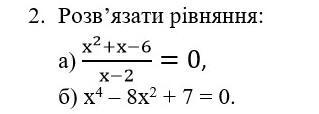
Ответы
Автор ответа:
2
Ответ:
а) -3
б)
Объяснение:
vasylua6:
б√7, це 6√7???
±√7
дякую
немає за що
Автор ответа:
1
Ответ:
a) -3 б) (±1; ±√7)
Объяснение:
x²+x-6/x-2=0
x≠2
x²+x-6=0
D = 25
x₁ = -3
x₂ ≠ 2
x⁴ - 8x²+7=0
x∈(±1; ±√7)
Похожие вопросы
Предмет: Русский язык,
автор: sssss43
Предмет: Русский язык,
автор: kristinakorolev
Предмет: Другие предметы,
автор: daniilanichkin
Предмет: Информатика,
автор: sakura8163