Question

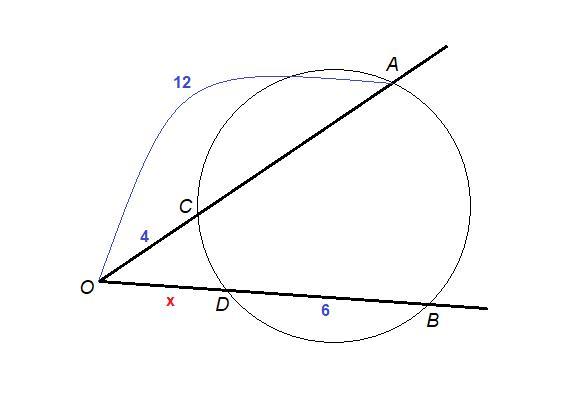
из точки О,лежавшей вне окружности,проведены две секущие ОА и ОВ,которые пересекают окружность в Точках С и D соответственно.Если ОС=4 см ОА=12 см и DB=6 см,найдите длину ОВ

Answer 1

Ответ:

ОВ = (√57 + 3) см

Объяснение:

Свойство отрезков секущих:

• произведения отрезков секущих, проведенных из одной точки, равны.

По свойству отрезков секущих:

OC · OA = OD · OB

Обозначим OD = x см.

ОС = 4 см,  ОА = 12 см

ОВ = х + 6  см

4 · 12 = x · (x + 6)

x² + 6x - 48 = 0

D = 6² + 4 · 48 = 36 + 192=228

√D = 2√57

$x=\dfrac{-6+2\sqrt{57}}{2}=\sqrt{57}-3$

$x=-\sqrt{57}-3$ - не подходит по смыслу задачи.

ОВ = OD + DB = √57 - 3 + 6 = √57 + 3 см