Опишите характер прямолинейного движения тела, представленного на графике в виде зависимости скорости υ от времени t (рис.). Используя кинематические соотношения, рассчитайте, чему равен путь: 1) за первые две
секунды движения; 2) за три секунды движения. Постройте график зависимости координаты x от времени t.
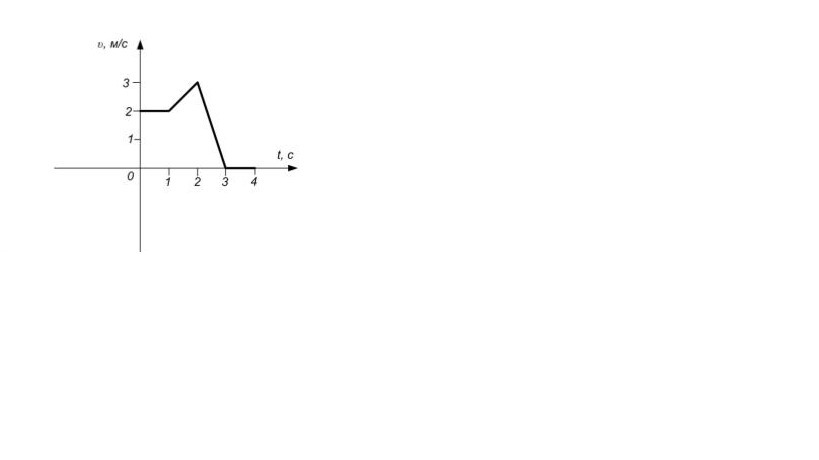
Ответы
характер движения :
0-1 сек - равномерное движение
1-2 сек - равноускоренное движение
3-3 сек - равнозамедленное движение
найдем пройденный путь за первую секунду
S1=V1*t1=2*1=2м Движение равномерное , график - прямая
Далее уравнение движения имеет вид S2=S1+V1*t+((a1)*(t2)^2)/2
где ускорение а1=(V2-V1)/t2 =3-2/1==1м/с^2
найдем пройденный путь за две секунды
S2=2+2*1+(1*1^2)/2=4.5 м Движение равноускоренное , график - парабола (так как уравнение квадратное) Знак при t^2 плюс - ветви в верх
Далее уравнение движения имеет вид S3=S2+V2*t3-((a2)*(t3)^2)/2
где ускорение а2=(V3-V2)/t3 =3-0/1 = 3м/с^2
найдем пройденный путь за три секунды
S3=4,5+3*1-(3*1^2)/2=6 м
Движение равнозамедленное , график - парабола (так как уравнение квадратное) Знак при t^2 минус - ветви у параболы направлены в низ.
1)за первые две секунды движения S2=4.5 м
; 2) за три секунды движения.
S3= 6 м
построим график.
По оси х = время t
По оси у = значение координат S
Рисунок приложить не могу, но дам координаты точек для построения.
(х:у)
Первая точка начало координат (0:0)
вторая точка (1:2) Между первой и второй точкой прямая.
третья точка (2:4,5) Между второй и третьей точкой график - парабола ветви в верх
четвертая точка (3:6) Между третьей и четвертой точкой график парабола ветви в низ
пятая точка (4:6) между четвертой и пятой точкой прямая.