Предмет: Математика,
автор: korolivskijizomrud
Докажите, что уравнение имеет только один корень
Приложения:
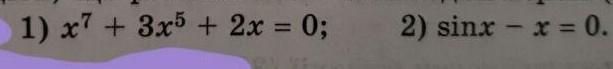
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1)
x^7+3x^5+2x = 0
(x^6+3x^4+2)*x = 0
x=0 или (x^6+3x^4+2) = 0
x^6 >=0
x^4 >= 0
x^6+3x^4+2 >=2
значит (x^6+3x^4+2) = 0 - не имеет решений
ответ
единственный корень x=0
2)
sin(x) - x =0
f(x)=sin(x)-x
f ` (x) = (cos(x) - 1) ∈ [-2;0]
f ` (x) <= 0 - значит f(x) - невозрастающая функция
причем f ` (x) = 0 только в отдельных точках (не на участках)
это значит что f(x) убывающая и это значит что f(x) = 0 имеет только единственный корень
Похожие вопросы
Предмет: Русский язык,
автор: Неуч123123
Предмет: Русский язык,
автор: Юра123458
Предмет: Английский язык,
автор: rtfhgfjjg
Предмет: Биология,
автор: diana1655