Question

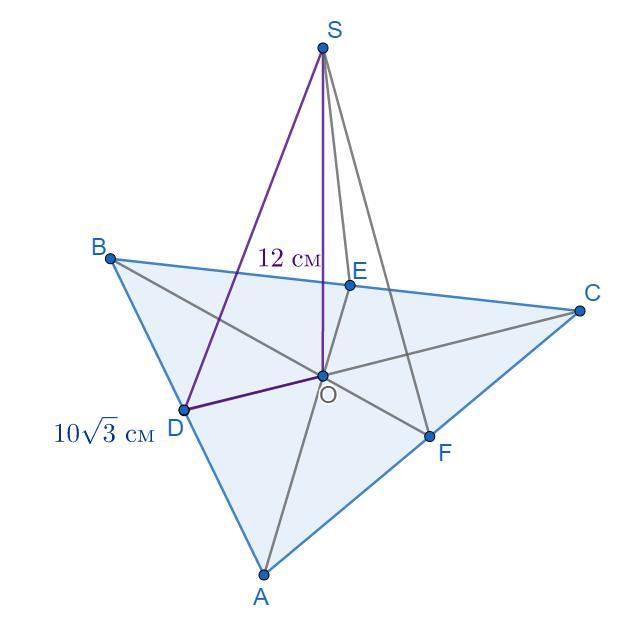
Сторона правильного трикутника дорівнює 10√3см деяка точка простору рівновіддалена від сторін трикутника і знаходиться на відстані 12см від площини трикутника .знайти відстань від цієї точки до сторони трикутника.

Answer 1

Ответ:

Расстояние от заданной точки до стороны треугольника равно 13 см.

Объяснение:

Сторона правильного треугольника равна 10√3 см. Некоторая точка пространства равноудалена от сторон треугольника и находиться на расстоянии 12 см от плоскости треугольника. Найти расстояние от этой точки до стороны треугольника.

Дано:
ΔABC равносторонний;

AB = 10√3 см;

SD = SE = SF (т.S равноудалена от сторон треугольника);

SO = 12 см (расстояние от т.S до плоскости ΔABC).

Найти: SD (расстояние от т.S до стороны треугольника).

Решение.

1) Расстояние от точки до плоскости равно длине перпендикулярного отрезка, проведенного из этой точки на плоскость.

SO ⊥ ΔABC.

• Основание перпендикуляра опущенного из точки, равноудаленной от сторон треугольника, лежит в центре вписанной в этот треугольник окружности.

• В равностороннем треугольнике его высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника.

• В равностороннем треугольнике центры вписанной и описанной окружности лежат в одной точке - центре равностороннего треугольника.

т.O лежит в точке пересечения медиан ΔABC.

2) Найдем длину отрезка BD.

В ΔABC проведем высоту СD.
CD - высота и медиана.

BD = AD = 10√3 : 2 = 5√3 (см).

4) Из прямоугольного ΔACD (∠D = 90°) по теореме Пифагора найдем катет CD.

CD² = AC² - AD²;

CD² = (10√3)² - (5√3)² = 300 - 75 = 225;

CD = 15 см.

5) Найдем длину отрезка OD.

Медианы треугольника пересекаются в одной точке и делятся  этой точкой в отношении 2 : 1, считая от вершины.

CD = 15 см,

CO : OD = 2 : 1;

OD = 15 : 3 · 1 = 5 см.

• Расстоянием от точки до прямой является длина перпендикуляра, опущенного из этой точки на прямую.
• Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

6) Найдем расстояние от точки S до стороны ΔABC.

BO - проекция наклонной SD в плоскости ΔABC.

BA ⊥ DO; ⇒ BA ⊥ SD.

Длина отрезка SD - это расстояние от точки S до стороны ΔABC.

ΔSDO прямоугольный, ∠SOD = 90°. По т.Пифагора найдем длину гипотенузы SD.

SD² = OD² + SO²;

SD² = 5² + 12² = 25 + 144 =169 = 13²;

SD = 13 см.

Расстояние от заданной точки до стороны треугольника равно 13 см.

#SPJ1