Question

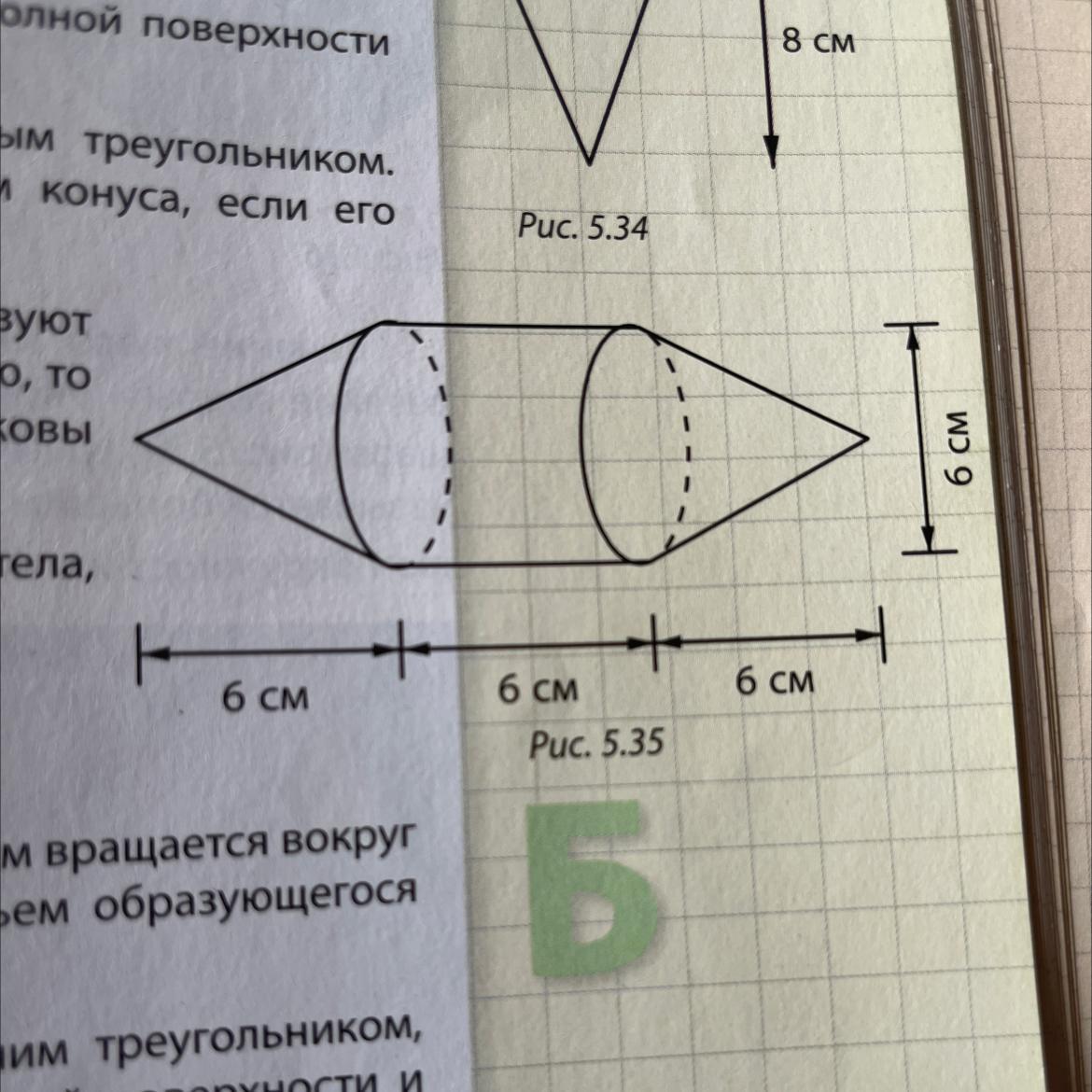
785. Найди объем и площадь полной поверхности тела,
изображенного на рисунке 5.35.

Answer 1

Ответ:

S фигуры = 395,64 (см^2)

V фигуры = 282,6 (м.куб)

Объяснение:

На рисунке изображена фигура состоящая из 2-ух конусов и по середине цилиндр. Длины их одинаковы = 6 см и ширина тоже = 6 см

S конуса = $S = \pi R^{2} + \pi RL$  S = 3,14 * $3^{2}$ + 3,14 * 3 * 9 = 28,26  + 84,78 = 113,04 (см^2)

L - образующая по теореме пифагора = $c^{2} = a^{2} + b^{2} = c = \sqrt{a^{2} } +b^{2}$

L = $\sqrt{} 3^{2} + 6^{2} = 9$

V объем конуса = $V = \frac{1}{3} \pi R^{2} * H$ = 1/3 * 3,14 * $3^{2}$ * 6 = 56,52 (м.куб)

Так конуса 2 (два) = S конуса = 113,04 * 2 = 226,08 (см^2)  V объем конуса = 56,52 * 2 = 113,04 (м.куб)

Найдем теперь цилиндр:

S цилиндра = $2\pi RH + 2\pi R^{2} = 2* 3,14 * 3 * 6 + 2* 3,14*3^{2} = 169,56$ (см^2)

V объем цилиндра = $\pi R^{2} H = 3,14 * 3^{2} *6 = 169,56$ (м.куб)

Складываем объем и площадь фигуры:

S фигуры = S конуса + S цилиндра = 226,08 + 169,56 = 395,64 (см^2)

V фигуры = V конуса + V цилиндра = 113,04 + 169,56  = 282,6 (м.куб)

Answer 2

Ответ:

фигуры = 395,64 (см^2)

V фигуры = 282,6 (м.куб)

Объяснение:

На рисунке изображена фигура состоящая из 2-ух конусов и по середине цилиндр. Длины их одинаковы = 6 см и ширина тоже = 6 см

S конуса = S = \pi R^{2} + \pi RLS=πR2+πRL  S = 3,14 * 3^{2}32 + 3,14 * 3 * 9 = 28,26  + 84,78 = 113,04 (см^2)

L - образующая по теореме пифагора = c^{2} = a^{2} + b^{2} = c = \sqrt{a^{2} } +b^{2}c2=a2+b2=c=a2+b2

L = \sqrt{} 3^{2} + 6^{2} = 932+62=9

V объем конуса = V = \frac{1}{3} \pi R^{2} * HV=31πR2∗H = 1/3 * 3,14 * 3^{2}32 * 6 = 56,52 (м.куб)

Так конуса 2 (два) = S конуса = 113,04 * 2 = 226,08 (см^2)  V объем конуса = 56,52 * 2 = 113,04 (м.куб)

Найдем теперь цилиндр:

S цилиндра = 2\pi RH + 2\pi R^{2} = 2* 3,14 * 3 * 6 + 2* 3,14*3^{2} = 169,562πRH+2πR2=2∗3,14∗3∗6+2∗3,14∗32=169,56 (см^2)

V объем цилиндра = \pi R^{2} H = 3,14 * 3^{2} *6 = 169,56πR2H=3,14∗32∗6=169,56 (м.куб)

Складываем объем и площадь фигуры:

S фигуры = S конуса + S цилиндра = 226,08 + 169,56 = 395,64 (см^2)

V фигуры = V конуса + V цилиндра = 113,04 + 169,56  = 282,6 (м.куб)