Предмет: Алгебра,
автор: dirdadimon
пожалуйста помогите решить!!!
Приложения:

Ответы
Автор ответа:
0
№1
a)
б)
в)
№2
а)
б)
№3
№4
a)
№5
Ответ:
№6
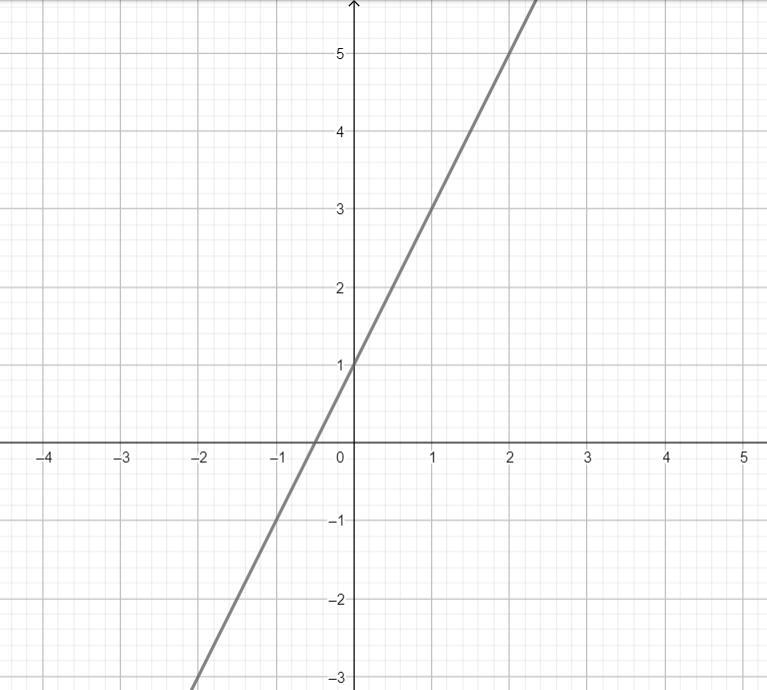
y = 2x + 1 - линейная функция, графиком является прямая
График на прикреплённой картинке
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Рокель11
Предмет: Английский язык,
автор: Soroka200000000
Предмет: Английский язык,
автор: darkangel24
Предмет: Математика,
автор: irmelina08
Предмет: Алгебра,
автор: lubimcevnikitka