Предмет: Математика,
автор: Lcashe
Очень срочно! Решить уравнение Коши
Приложения:
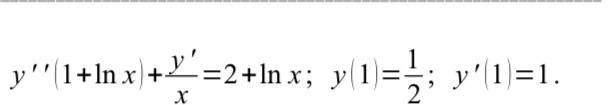
Ответы
Автор ответа:
1
Ответ:
Решением задачи Коши является функция y=x²/2
Пошаговое объяснение:
Отметим, что - вычисляется заменой t=ln x.
Тогда
Значит
по условию y'(1)=1 - подставим в уравнение и найдем C₁:
1*(1+0)=1*ln 1 +1+C₁
1=1+C₁
C₁=0
По условию y(1)=1/2 - подставляем и находим C:
1/2=1/2+C
C=0
Значит y=x²/2
PS: Выше, в уравнении для y', мы сокращали на выражение 1+ln x
оно обращается в ноль при x=e⁻¹ (тогда сокращать на 1+ln x нельзя). Легко проверить, что для найденной функции y=x²/2 нет никаких проблем в этой точке и она удовлетворяет уравнению для любых x>0. (это область определения логарифма)
#SPJ1
solka0000:
будь ласка , допоможіть мені з математикою , якщо маєте час , додала в свої питання вже і даю максимум балів ,
Похожие вопросы
Предмет: Русский язык,
автор: dukhova1988
Предмет: Окружающий мир,
автор: диана1767
Предмет: Окружающий мир,
автор: Lerok377
Предмет: Математика,
автор: irmelina08
Предмет: Алгебра,
автор: lubimcevnikitka