Предмет: Алгебра,
автор: sobrik2005
найдите наименьшее и наибольшее значение функции на отрезке
Приложения:
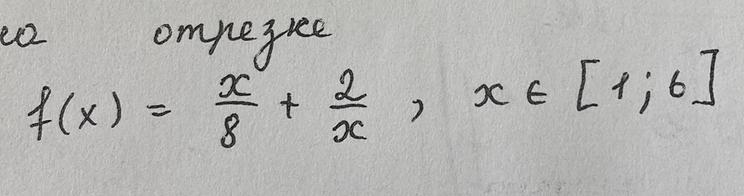
Ответы
Автор ответа:
0
Ответ: min f( x ) = f( 4 ) = 1 ; max f( x ) = f( 1 ) = 2 1/8 .
[ 1 ; 6 ] [ 1 ; 6 ]
Объяснение:
# f( x ) = x/8 + 2/x ; xЄ [ 1 ; 6 ] .
f '( x ) = ( x/8 + 2/x )' = 1/8 - 2/x² = ( x² - 16 )/(8x² ) = ( x + 4 )( x - 4 )/( 8x² ) ;
f '( x ) = 0 ; ( x + 4 )( x - 4 )/( 8x² ) = 0 ;
x₁ = 4 ; x₂ = - 4∉ [ 1 ; 6 ] .
f( 1 ) = 1/8 + 2/1 = 2 1/8 ; f( 4 ) = 4/8 + 2/4 = 1/2 + 1/2 = 1 ;
f( 6 ) = 6/8 + 2/6 = 3/4 + 1/3 = 1 1/12 .
min f( x ) = f( 4 ) = 1 ; max f( x ) = f( 1 ) = 2 1/8 .
[ 1 ; 6 ] [ 1 ; 6 ]
Похожие вопросы
Предмет: Английский язык,
автор: Ёка2004
Предмет: Русский язык,
автор: Cofo4ka
Предмет: Английский язык,
автор: poteto1
Предмет: История,
автор: fytew467
Предмет: Математика,
автор: тусикк