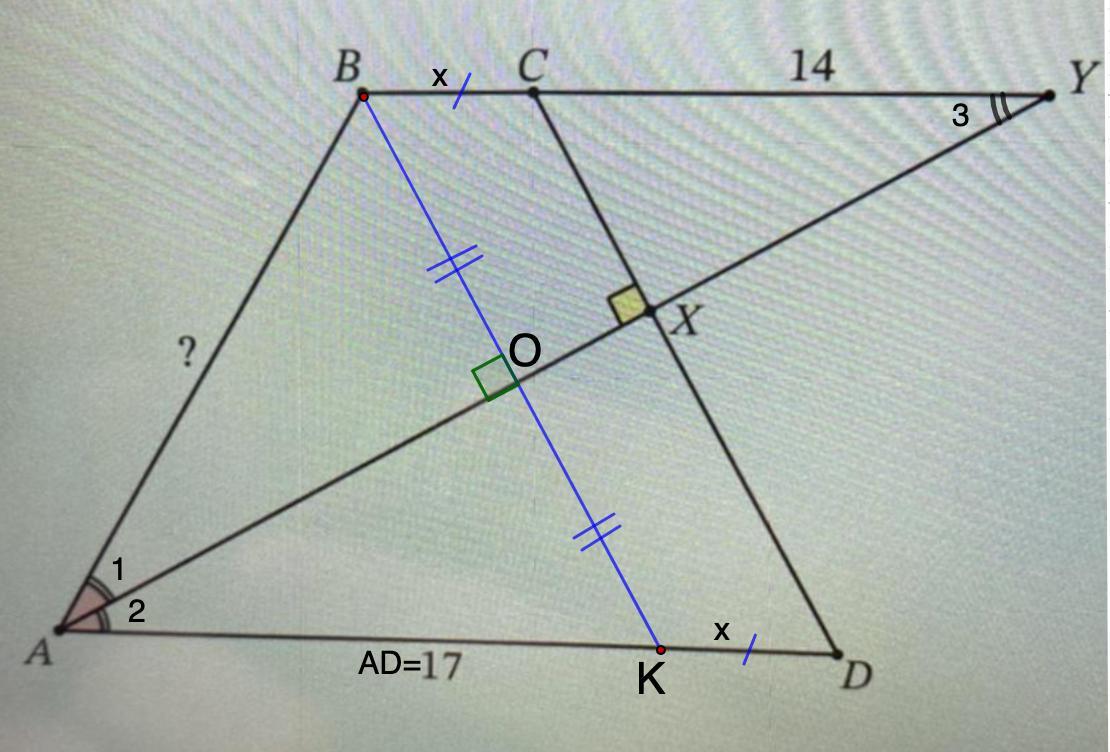
Дан четырёхугольник ABCD, в котором AD∥BC. Биссектриса угла A пересекает сторону CD в точке X, а продолжение стороны BC за точку C —— в точке Y. Оказалось, что ∠AXC=90∘
Найдите длину отрезка AB, если известно, что AD=17 и CY=14.
Ответы
Ответ:
Длина отрезка АВ равна 15,5 ед.
Пошаговое объяснение:
Дан четырёхугольник ABCD, в котором AD∥BC. Биссектриса угла A пересекает сторону CD в точке X, а продолжение стороны BC за точку C - в точке Y. Оказалось, что ∠AXC=90∘
Найдите длину отрезка AB, если известно, что AD=17 и CY=14.
Дано: ABCD - четырёхугольник;
AD || BC;
AY - биссектриса ∠А;
∠AXC=90°;
AD = 17; CY = 14.
Найти: АВ.
Решение.
Проведем ВК || CD.
1. Рассмотрим ΔABY.
∠1 = ∠2 (AY - биссектриса)
∠3 = ∠2 (накрест лежащие при BY || AD и секущей AY)
⇒∠1 = ∠3
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ ΔABY - равнобедренный.
АВ = BY
CD ⊥ AY (условие); ВК || CD (построение)
- Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.
⇒ BO ⊥ AY
⇒ ВО - высота
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой.
⇒ АО = ОY.
2. Рассмотрим ΔАВК.
АО - биссектриса.
BК ⊥ AY (п.1)
⇒ АО - высота.
- Если в треугольнике высота является биссектрисой, то этот треугольник равнобедренный.
⇒ АО - медиана;
⇒ ВО = ОК.
3. Рассмотрим ΔАОК и ΔВОY - прямоугольные.
АО = ОY (п.1)
ВО = ОК (п.2)
ΔАОК = ΔВОY (по двум катетам)
⇒ BY = AK (как соответственные элементы)
4. Рассмотрим ВСDK.
ВС || KD (условие)
ВК || CD (построение)
⇒ ВСDK - параллелограмм (по определению).
Противоположные стороны параллелограмма равны.
⇒ ВС = KD
5. Пусть ВС = KD = х
BY = AK (п.3)
или
х + 14 = 17 - х
2х = 3
х = 1,5
⇒ АВ = BY = 1,5 + 14 = 15,5
Длина отрезка АВ равна 15,5 ед.
#SPJ1