Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
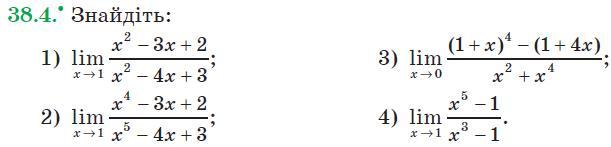
Ответы
Автор ответа:
0
Ответ:
1)
2)
3)
4)
Примечание:
если
существует в точке
------------------------------------------------------------------------------------------------------
Если:
1)
2) функции и
дифференцируемы в окрестности точки
3)
По правилу Лопиталя:
Объяснение:
1)
2)
3)
4)
Похожие вопросы
Предмет: Русский язык,
автор: fixpro12
Предмет: Русский язык,
автор: ureew
Предмет: Английский язык,
автор: LKKK
Предмет: Литература,
автор: 1011vlad1011
Предмет: Алгебра,
автор: pozivnoynapoleon