Предмет: Геометрия,
автор: devazqj182
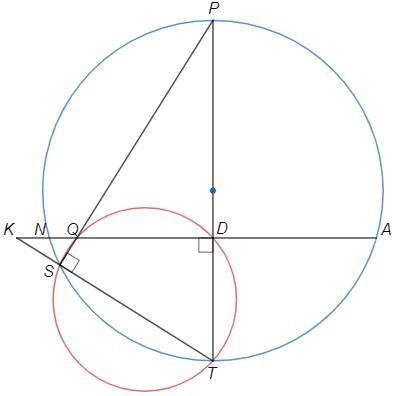
В произвольном остроугольном треугольнике КРТ высоты KD и PS пересекаются в точке Q. Через точки P, S, T проведена окружность, пересекающая KD в точке N, причём ND = 30, кQ = 11.
Найдите KD
найдите KN
Найдите NQ
Ответы
Автор ответа:
3
В прямоугольном △PST гипотенуза PT является диаметром описанной окружности. Диаметр PT перпендикулярен хорде NA, следовательно делит ее пополам, ND=DA=30.
SQDT - вписанный (противоположные углы прямые).
Произведение секущей на ее внешнюю часть постоянно для данной точки и данной окружности.
KN*KA=KS*KT (синяя окружность)
KQ*KD=KS*KT (красная окружность)
=> KN*KA=KQ*KD
KN=x
x(x+60) =11(x+30) => x^2 +49x -330 =0
x = √(49^2 +4*330) -49 /2 =6 (x>0)
KN=6, NQ=5, KD=36
Приложения:
orjabinina:
Добрый вечер, siestarjoki. Верно ли утверждение" Если треугольники подобны , то радиусы описанных окружностей , около этих треугольников , относятся как коэффициент подобия"?
да, конечно
вообще все соответствующие отрезки относятся как коэффициент подобия
то есть все, что построено по одному алгоритму относительно равных углов
Спасибо.
только D - не центр, надо исправить. Диаметр PT перпендикулярен хорде NA и делит ее пополам.
нажмите флажок
Похожие вопросы
Предмет: Английский язык,
автор: tatatrusova82
Предмет: Русский язык,
автор: ProstoNecto
Предмет: Немецкий язык,
автор: bylkincaschakopa
Предмет: Русский язык,
автор: Reiny