Знайти проміжки зростання і спадання та екстремуми функції
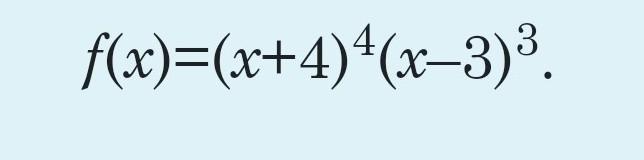
Ответы
Объяснение:
Поглянь на фото рішення де я вам додаю

найдем производную функции f(x)=(x+4)⁴(x-3)³
f'(x)=4*(x+4)³(x-3)³+3*(x-3)²*(x+4)⁴=(x+4)³(x-3)²*(4x-12+3x+12)=
7x(x+4)³(x-3)²
решим методом интервалов, например, такое неравенство
f'(x)≤0, выяснив автоматически как промежутки возрастания. так и промежутки убывания. а также и экстремумы, т.е. максимум и минимум функции.
7x(x+4)³(x-3)²≤0
найдем корни левой части неравенства.
х=0;
х+4=0
х=-4
х-3=0
х=3
нанесем точки в порядке возрастания на числовую ось.
_____-4________0__________3___
смотрим на коэффициенты при х : 7; 1;1- все положительны , поэтому
начинаем ставить знаки с правой стороны,
т.к. 7*1*1 больше нуля, то начинаем с плюса.
_____-4________0__________3___
+
затем смотрим на корень 3, его нам дала скобка (x-3)² - в четной степени, поэтому знак не меняется. остается при переходе через 3, тоже положительным
_____-4________0__________3___
+ +
следующий корень х=0 в разложении он в нечетной первой степени, поэтому при переходе через ноль меняем знак с плюса на минус
_____-4________0__________3___
- + +
и наконец х=-4, этот корень нам дал множитель (x+4)³ в нечетной третьей степени, поэтому знак меняем
с минуса на плюс
_____- 4________0__________3___
+ - + +
промежутки, в которых производная положительна, - это промежутки возрастания, (-∞;-4) и [0; +∞) - промежутки возрастания, а при х∈ [-4;0] функция убывает.
х=-4 - точка максимума, при переходе через нее производная меняет знак с плюса на минус. максимум функции
f(x)=(x+4)⁴(x-3)³ равен
f(-4)=(-4+4)⁴(-4-3)³ равен 0
критическая точка х=3- не является экстремальной. т.к. при переходе через нее производная знак не меняет.
х=0- точка минимума, т.к. производная при переходе через эту точку меняет знак с минуса на плюс.
Минимум функции
f(x)=(x+4)⁴(x-3)³ равен
f(0)=(0+4)⁴(0-3)³=256*(-27)=-6912
Р.S
если речь о строгом возрастании. то ставим круглые скобки. а если о нестрогом, то квадратные. Объясню, почему я поставил квадратные. В условии дан многочлен, областью его определения является вся числовая прямая, поэтому функция непрерывна, и точки минус 4, ноль и три вошли в промежутки монотонности.