Предмет: Алгебра,
автор: msTen
Плиз! Представьте выражение в виде степени с основанием b
Приложения:
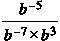
Ответы
Автор ответа:
1
Ответ: 1/b
msTen:
там только варианты b⁰, b⁻¹, b⁻³ и b⁵
b в степени -1. Это одно и тоже. Выбери b в степени минус 1
Спасибо!
пожалуйста )))
Автор ответа:
1
Ответ:
Пользуемся свойствами степеней.
там только варианты b⁰, b⁻¹, b⁻³ и b⁵
дописала вариант ответа с отрицат. показателем
Спасибо)
то есть знай, что b⁻¹=1/b
Ага, запомню :з
Похожие вопросы
Предмет: Английский язык,
автор: анна1259
Предмет: Русский язык,
автор: поит
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: iod5550
Предмет: Математика,
автор: daniilmarushko