Question

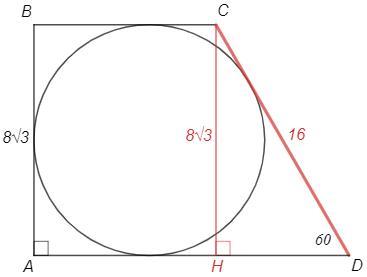
меньшая боковая сторона прямоугольной трапеции равна 8 корней из 3 см,а острый угол 60 градусов .Найдите площадь трапеции ,если известно,что в неё можно вписать окружность
НУЖНО РЕШЕНИЕ НЕ ЧЕРЕЗ СИНУСЫ И КОСИНУСЫ
даю 30 баллов

Answer 1

Площадь трапеции - полусумма оснований на высоту.

S =1/2 (BC+AD) h

Высота известна: так как трапеция прямоугольная, меньшая боковая сторона перпендикулярна основаниям.

h =AB =8√3

Трапеция описанная. В описанном четырехугольнике суммы противоположных сторон равны.

BC+AD =AB+CD

Осталось найти CD.

Опустим высоту CH и рассмотрим треугольник CDH.

∠HСD =90°-60° =30°

Катет против угла 30° равен половине гипотенузы, HD=CD/2

Пусть HD=x, CD=2x, тогда по т Пифагора

CH =√(CD^2-HD^2) =x√(4-1) =x√3

CH/CD =√3/2 => CD=8√3 :√3/2 =16

Таким образом

S =1/2 (8√3 +16) 8√3 = 96+64√3 (см^2)