Предмет: Геометрия,
автор: bezimeni50
найдите площадь сечения правильной четырёхугольной пирамиды плоскостью, проходящей через середины трех её боковых сторон, если сторона основания пирамиды равна 22
Ответы
Автор ответа:
1
Ответ:
Площадь сечения 121 кв. ед.
Объяснение:
Основание правильной четырехугольной пирамиды - квадрат, боковые грани - равные равнобедренные треугольники.
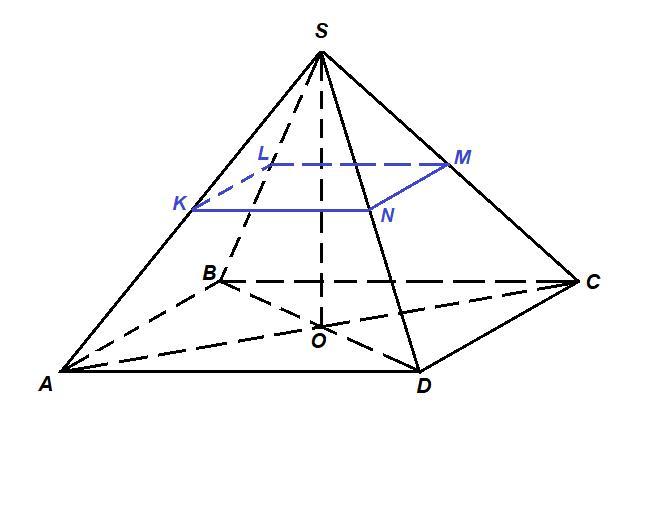
Пусть точки К, L, M - середины боковых ребер SA, SB и SC соответственно.
KL и LM - отрезки сечения.
KL║AB и LM║BC как средние линии соответствующих треугольников.
Тогда плоскость (KLM)║(ABC) по признаку параллельности плоскостей.
Проведем МN и NK - средние линии треугольников SCD и SAD.
KLMN - искомое сечение.
Стороны четырехугольника равны, так как являются средними линиями равных треугольников. Углы его равны по 90° (они равны углам основания как углы с соответственно параллельными сторонами), значит KLMN - квадрат.
KL = 0,5 AB = 0,5 · 22 = 11
Приложения:
bezimeni50:
спасибо
Похожие вопросы
Предмет: Русский язык,
автор: вика6769
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: анастас20041
Предмет: Английский язык,
автор: mido20
Предмет: Английский язык,
автор: loginkyn