Предмет: Геометрия,
автор: SVKB
Допоможіть, будь ласка . Даю 50 балів
Приложения:

Ответы
Автор ответа:
1
Ответ:
1. x = a sinα
2.
3.
Объяснение:
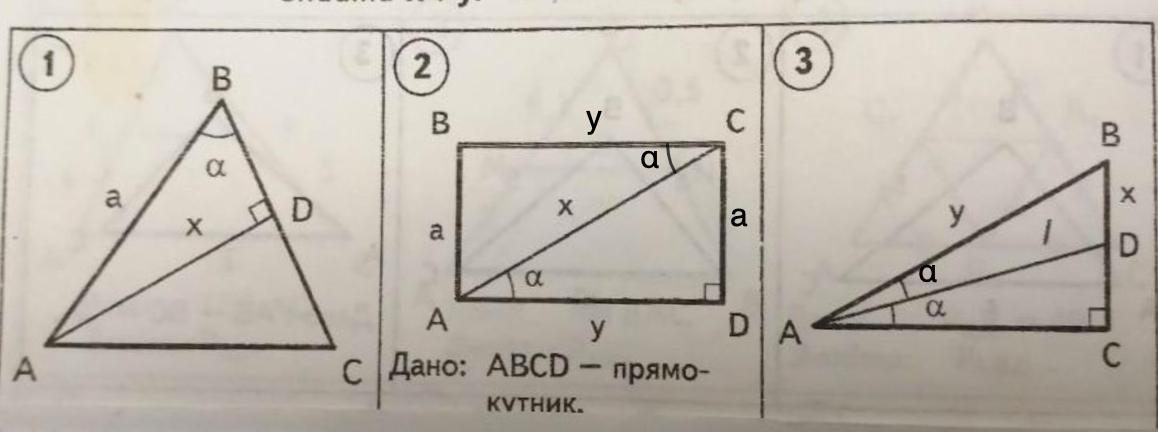
Выполнить задания по готовым чертежам.
Найти х и у.
1. Рассмотрим Δ ABD - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
2. Рассмотрим ΔACD - прямоугольный.
- Противоположные стороны прямоугольника равны.
⇒ DC = AB = a
- Тангенс угла - отношение противолежащего катета е прилежащему.
3. Рассмотрим ΔADC - прямоугольный.
Выразим DC и AC.
- Косинус угла - отношение прилежащего катета к гипотенузе.
Рассмотрим ΔАВС - прямоугольный.
AD - биссектриса ⇒ ∠BAD = ∠DAC = α ⇒ ∠A = 2α
#SPJ1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: вика6769
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: анастас20041
Предмет: Английский язык,
автор: mido20
Предмет: Английский язык,
автор: loginkyn