Question

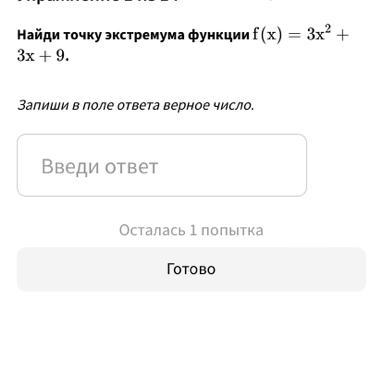
Решите пожалуйста……………

Answer 1

Ответ:

решение смотри на фотографии

Answer 2

$\displaystyle\bf\\f(x)=3x^{2} +3x+9$

Найдём производную :

$\displaystyle\bf\\f'(x)=3\cdot(x^{2} )'+3\cdot x'+9'=3\cdot 2x+3\cdot 1+0=6x+3$

Приравняем производную нулю , найдём критические точки :

$\displaystyle\bf\\6x+3=0\\\\6x=-3\\\\x=-0,5$

Отметим критическую точку на числовой оси и определим знаки производной функции в полученных интервалах.

          -                                    +

____________ - 0,5 _____________

                            min

x = - 0,5 - точка минимума , так как при переходе через эту точку производная меняет знак  с " - "  на  " + " .

$\displaystyle\bf\\f(-0,5)=3\cdot(-0,5)^{2} +3\cdot(-0,5)+9=0,75-1,5+9=8,25$